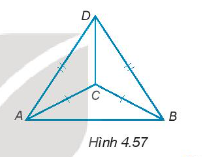
Cho các điểm A, B, C, D như Hình 4.57.
Đường thẳng DC có vuông góc với đường thẳng AB không? Vì sao?
Giải bởi Vietjack
Hướng dẫn giải
Ta có: DA = DB nên D cách đều A và B, do đó D thuộc đường trung trực của đoạn thẳng AB.
Tương tự CA = CB nên C cách đều A và B, do đó C thuộc đường trung trực của đoạn thẳng AB.
Vậy đường thẳng DC là đường trung trực của đoạn thẳng AB.
Do đó đường thẳng DC vuông góc với đường thẳng AB.
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Chứng minh rằng MP = MQ và AP = AQ.
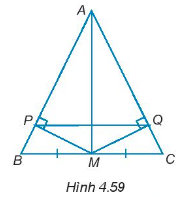
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC (H.4.59).
Đường thẳng PQ có vuông góc với AM không? Vì sao?
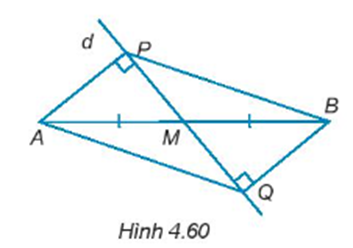
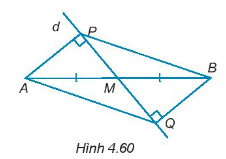
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
∆APB = ∆BQA.
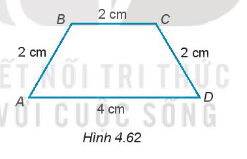
Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.
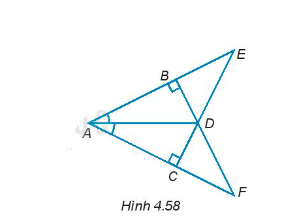
Cho các điểm A, B, C, D, E, F như Hình 4.58.
Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
AP = BQ.
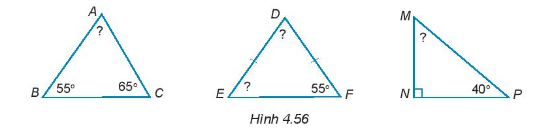
Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
