Tìm chữ số thích hợp cho dấu hỏi chấm: a) -5,02

Question

Tìm chữ số thích hợp cho : a) −5,02<−5,?1b) −3,7?8>−3,715c) −0,5?742<−0,59653;d) −1,4?<−1,49

VietJack · Accepted Answer

a) Vì −5,02<−5,?1 nên 5,02 > 5, ?1. Ta xét hai số 5,02 và 5,?1 thấy phần nguyên của hai số giống nhau nên để số 5,02 > 5, ? 1 thì ? phải điền số 0 vì nếu là số lớn hơn 0 thì không thỏa mãn. b) Vì −3,7?8>−3,715 nên 3,7 ?8 < 3,715. Ta xét hai số 3,7 ? 8 và 3,715 thấy phần nguyên và hàng phần mười của hai số giống nhau; hàng phần nghìn có 8 > 5 nên hàng phần trăm của 3,7 ? 8 phải nhỏ hơn hàng phần trăm của 3,715. Do đó ? chỉ có thể là 0. c) Vì −0,5?742<−0,59653 nên 0,5 ?(742) > 0,59653. Ta xét hai số 0,5 ?(742) và 0,59653 thấy phần nguyên và hàng phần mười của hai số giống nhau nếu nhỏ hơn 9 thì 0,5 ?(742) < 0,58653 nên ? chỉ có thể là 9. d) Vì −1,4?<−1,49 nên 1,4? > 1,49 Ta có: 1,4?=1,4?4?... ta thấy nếu ? < 9 thì 1,4?=1,4?4?... < 1,49 nên ?chỉ có thể là 9.

Câu hỏi:

Tìm chữ số thích hợp cho :

$a) - 5, 02 < - 5, ? 1 b) - 3, 7 ? 8 > - 3, 715 c) - 0, 5 ? (742) < - 0, 59653; d) - 1, (4 ?) < - 1, 49$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

$a) N ế u a \in ℤ t h ì a \in ℝ b) N ế u a \in ℚ t h ì a \in ℝ c) N ế u a \in ℝ t h ì a \in ℤ d) N ế u a \in ℝ t h ì a \notin ℚ$

Câu 2:

So sánh:

a) –1,(81) và –1,812;

b) $2 \frac{1}{7}$ và 2,142;

c) –48,075… và –48,275…;

d) $\sqrt{5}$ và $\sqrt{8}$

Câu 3:

a) Sắp xếp các số sau theo thứ tự tăng dần:

–2,63…; 3,(3); –2,75…; 4,62.

b) Sắp xếp các số sau theo thứ tự giảm dần:

1,371…; 2,065; 2,056…; –0,078…;1,(37).

Câu 4:

So sánh hai số thực sau:

$a) 1, (375) v à 1 \frac{3}{8} b) - 1, (27) v à - 1, 272 .$

Câu 5:

Tìm số đối của mỗi số sau: $\frac{2}{- 9}; - 0, 5; - \sqrt{3}$

Câu 6:

a) Nếu hai ví dụ về số hữu tỉ.

b) Nêu hai ví dụ về số vô tỉ.

Câu 7:

Câu 8:

Biểu diễn các số hữu tỉ sau trên trục số: $\frac{- 1}{2}; 1; 1, 25; \frac{7}{4}$ .

Câu 9:

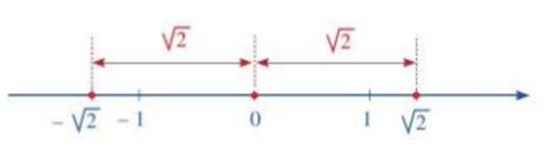
a) So sánh hai số thập phân sau: –0,617 và –0,614.

b) Nêu quy tắc so sánh hai số thập phân hữu hạn.

Câu 10:

Các số hữu tỉ và vô tỉ được gọi chung là số gì?

Câu 11:

Tìm số đối của mỗi số sau: $\frac{- 8}{35}; \frac{5}{- 6}; - \frac{18}{7}; 1, 15; - 21, 54; - \sqrt{7}; \sqrt{5}$

Câu 12:

a) Nêu biểu diễn thập phân của số hữu tỉ.

b) Nêu biểu diễn thập phân của số vô tỉ.

Đề thi liên quan

Câu hỏi mới nhất