So sánh:
a) –1,(81) và –1,812;
b) và 2,142;
c) –48,075… và –48,275…;
d) và
 Giải bởi Vietjack
Giải bởi Vietjack
a) Hai số cần so sánh là hai số âm nên ta đi so sánh số đối của chúng.
Số đối của –1,(81) là 1,(81).
Số đối của –1,812 là 1,812.
Ta có: 1,(81) = 1, 8181…
So sánh: 1,8181…và 1,812 ta thấy: Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần nghìn. Mà 8 > 2 nên 1,8181… > 1,812.
Do đó –1,8181… < –1,812 hay –1,(81) < 1,812.
b) Ta thấy và 2,142 có phần nguyên giống nhau nên ta đi so sánh và 0,142.
Ta thực hiện đặt phép tính chia 1 cho 7 như sau:

Vậy
Ta so sánh 0,1428… và 0,1420
Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau là cặp chữ số hàng phần chục nghìn. Mà 8 > 0 nên 0,1428… > 0,1420 hay .
c) Hai số cần so sánh là hai số âm nên ta đi so sánh hai số đối của chúng.
Số đối của –48,075… là 48,075…
Số đối của –48,275… là 48,275…
Ta so sánh 48,075… và 48,275…
Kể từ trái sang phải, cặp số cùng hàng đầu tiên khác nhau là cặp số hàng phần mười. Mà 0 < 2 nên 48,075… < 48,275…Do đó –48,075… > –48,275…
d) Vì 8 > 5 > 0 nên .
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Sắp xếp các số sau theo thứ tự tăng dần:
–2,63…; 3,(3); –2,75…; 4,62.
b) Sắp xếp các số sau theo thứ tự giảm dần:
1,371…; 2,065; 2,056…; –0,078…;1,(37).
Đọc kỹ nội dung sau:
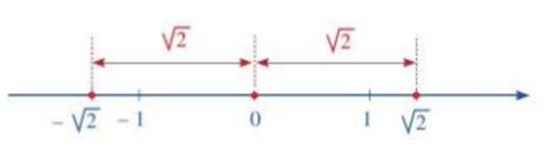
Gọi A là điểm (nằm bên phải điểm gốc 0) biểu diễn số thực trên trục số nằm ngang. Gọi B là điểm nằm bên trái điểm gốc 0 sao cho OA = OB (điểm biểu diễn điểm gốc 0). Khi đó, điểm B biểu diễn một số thực, kí hiệu là .
a) So sánh hai số thập phân sau: –0,617 và –0,614.
b) Nêu quy tắc so sánh hai số thập phân hữu hạn.
a) Nêu biểu diễn thập phân của số hữu tỉ.
b) Nêu biểu diễn thập phân của số vô tỉ.