Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:
EM > ED.
Giải bởi Vietjack
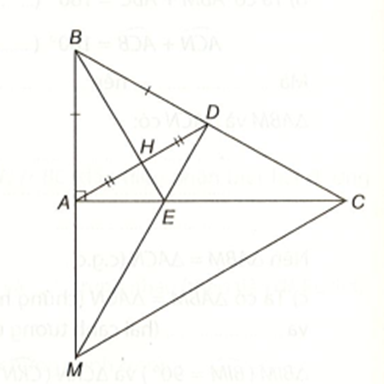
∆BAE = ∆BDE (chứng minh trên) nên \(\widehat {BDE} = \widehat {BAE} = 90^\circ \).
∆EAM và ∆EDC có:
\(\widehat {EAM} = \widehat {EDC} = 90^\circ \),
EA = ED (chứng minh trên),
\(\widehat {AEM} = \widehat {DEC}\) (hai góc đối đỉnh).
Nên ∆EAM = ∆EDC (g.c.g). Suy ra EM = EC.
∆EDC vuông tại D nên EC > ED (quan hệ giữa cạnh và góc trong tam giác).
Mà EC = EM (chứng minh trên) nên EM > ED.
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.
Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.
Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng AN // BC.
Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC.
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:
Tam giác BCM là tam giác đều và CE = 2EA, biết \[\widehat {ABC}\] = 60°.
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:
∆ABH = ∆DBH.
Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC.
Gọi I là điểm trên AM, K là điểm trên AN sao cho BI ⊥ AM; CK ⊥ AN. Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK // MN.
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho BD = BA và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt tia BA tại M. Chứng minh rằng:
Tam giác AED cân.
Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC.
Chứng minh AH ⊥ BC.
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
