Một tam giác có ba cạnh là 52; 56; 60. Bán kính đường tròn ngoại tiếp là:
A. 32,5
B. 32
C. 36
D. Đáp án khác
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
Ta có nửa chu vi của tam giác đã cho là:
P = (52 + 56 + 60) : 2 = 84
Suy ra:
Mà
Phương pháp giải
Cho tam giác ABC, ta kí hiệu độ dài các cạnh là a=BC, b=CA, c=AB, các góc của tam giác được viết đơn giản là A,B,C. Diện tích tam giác được kí hiệu là S.
Gọi độ dài đường cao (chiều cao) hạ từ các đỉnh A,B,C lần lượt là ha, hb, hc.
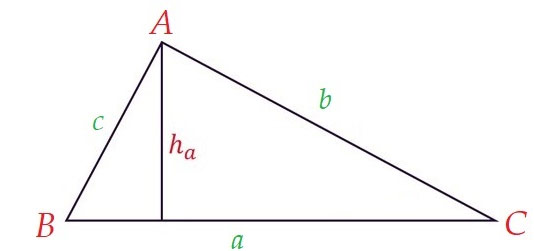
Đặc biệt:
Diện tích tam giác vuông tại A là:
Diện tích tam giác cân tại A là: (với H là trung điểm của BC).
Diện tích tam giác đều cạnh a là:
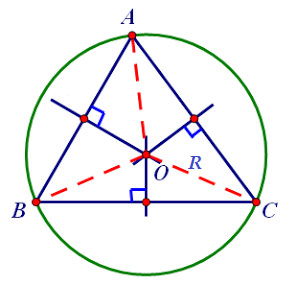
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Ta có:
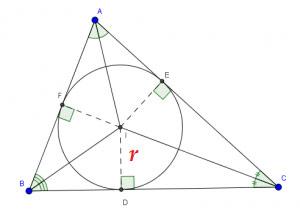
Gọi r là bán kính đường tròn nội tiếp tam giác ABC và p là nửa chu vi tam giác ():
Với p là kí hiệu nửa chu vi như ở mục 4, ta có:
Trong mặt phẳng Oxy, gọi tọa độ các đỉnh của tam giác ABC là: A(xA,yA),B(xB,yB),C(xC,yC).
Khi đó:
Áp dụng trong không gian, với khái niệm tích có hướng của 2 vectơ. Ta có:
Xem thêm một số kiến thức liên quan:
Tổng hợp công thức tính diện tích hình tam giác đầy đủ, chi tiết nhất
Cho tam giác ABC có A(5;3) : B(2;-1) và C(-1; 5). Tính tọa độ chân đường cao vẽ từ A.
Cho tam giác ABC có b = 7; c = 5, cosA = 3/5. Đường cao ha của tam giác ABC là
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 600. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một cái ao. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 78024’ . Biết CB = 120m và CA = 250 m. Khoảng cách AB bằng bao nhiêu ?
Cho tam giác ABC có A(5;3); B(2;-1) và C(-1; 5). Tìm tọa độ trực tâm tam giác ABC.
Gọi ![]() là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ?
là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng ?
Cho các điểm A(1;1) ; B( 2;4) và C(10; -2) . Góc BAC bằng bao nhiêu độ?
Biết A(1;-1) và B(3;0) là hai đỉnh của hình vuông ABCD. Tìm tọa độ các đỉnh C ?
Cho hình chữ nhật ABCD biết AD = 1 . Giả sử E là trung điểm AB và thỏa mãn .Tính độ dài cạnh AB.
Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Cho tam giác ABC thỏa mãn sin2A = sinB. sinC. Hỏi mệnh đề nào đúng.