Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 dm3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng / m3. Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó phải trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
A. 1.08 triệu đồng.
B. 0,91 triệu đồng
C. 1,68 triệu đồng
D. 0,54 triệu đồng
Giải bởi Vietjack
Đáp án A.
Gọi x(x>0) chiều rộng của đáy bể.
+ Chiều dài của đáy bể là 2x.
+ Chiều cao của bể là .
Xét .
Ta có .
Từ bảng biến thiên ta có .
Vậy chi phí thấp nhất để thuê nhân công xây bể là 2,16.500000 = 1080000 đồng
Phương pháp giải
Ta thường dùng một trong các phương pháp sau:
* Phương pháp 1: Sử dụng các bất đẳng thức cơ bản
∀x ∈ ℝ, n ∈ ℕ* ta luôn có:
√ –1 ≤ sin x ≤ 1, –1 ≤ sin2n + 1x ≤ 1.
√ –1 ≤ cos x ≤ 1, –1 ≤ cos2n + 1x ≤ 1.
√ 0 ≤ |sin x| ≤ 1, 0 ≤ sin2nx ≤ 1.
√ 0 ≤ |cos x| ≤ 1, 0 ≤ cos2nx ≤ 1.
* Phương pháp 2: Sử dụng định nghĩa
Cho hàm số y = f(x) xác định trên miền D.
+ Số thực dương M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu:
.
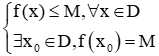
+ Số thực dương m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu:
.
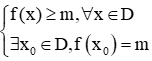
* Phương pháp 3: Lập bảng biến thiên hoặc vẽ đồ thị của hàm số, từ đó rút ra kết luận.
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay, chọn lọc
Một hộp có chứa 8 bóng đèn màu đỏ và 5 bóng đèn màu xanh. Số cách chọn được một bóng đèn trong hộp đó là
Cho hàm số y=f(x) có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
Cho hàm số y=f(x) có bảng biến thiên như sau:
Kết luận nào sau đây đầy đủ về đường tiệm cận của đồ thị hàm số y=f(x)?
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Cho khối lăng trụ tam giác đều ABC.A'B'C'. Các mặt phẳng (AB'C) và (A'BC') chia lăng trụ thành 4 phần. Thể tích phần nhỏ nhất trong 4 phần được tạo ra bằng bao nhiêu thể tích V của lăng trụ bằng 1?
Trong không gian với hệ tọa độ Oxyz cho mặt cầu . Biết khi m thay đổi thì (S) luôn chứa một đường tròn cố định. Bán kính đường tròn đó bằng
Cho đồ thị hàm số y=f(x) như hình vẽ. Số điểm cực trị của hàm số là
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
