Một chiếc máy quay phim ở đài truyền hình được đặt trên một giá đỡ ba chân với điểm đặt P(0; 0; 4) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là Q₁(0; – 1; 0), Q_{2 $\left(\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$}, Q_{3 $\left(-\frac{\sqrt{3}}{2};\frac{1}{2};0\right)$} (Hình 35). Biết rằng trọng lượng của máy quay là 360 N.

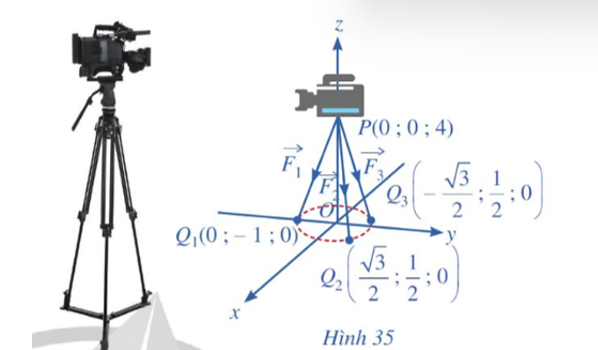
Làm thế nào để tìm được tọa độ của các lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$  tác dụng lên giá đỡ?

b) Tính chu vi tam giác ABC.

Trong không gian với hệ tọa độ Oxyz, cho hai vectơ $\overrightarrow{u}=\left(1;0;-3\right)$  và $\overrightarrow{v}=\left(0;0;3\right)$ . Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{w}$   khác $\overrightarrow{0}$  vuông góc với cả hai vectơ $\overrightarrow{u}$  và $\overrightarrow{v}$  .

b) Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có trọng tâm G.

Ÿ Biểu diễn vectơ $\overrightarrow{OG}$  theo hai vectơ $\overrightarrow{OA}$  ,$\overrightarrow{OB}$ , $\overrightarrow{OC}$  .

Ÿ Tính tọa độ của điểm G theo tọa độ của các điểm A(x_A; y_A; z_A), B(x_B; y_B; z_B), C(x_C; y_C; z_C).

Cho ba điểm A(0; – 1; 1), B(1; 0; 5), G(1; 2; 0).

a) Chứng minh rằng ba điểm A, B, G không thẳng hàng.

b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2; – 1; 1), B(1; – 1; 2) và C(3; 0; 2). Chứng minh rằng tam giác ABC vuông tại A.

a) Cho hình lập phương ABCD.A'B'C'D' có A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), C'(1; 1; 1). Hãy chỉ ra tọa độ của một vectơ vuông góc với cả hai vectơ $\overrightarrow{AB}$  và $\overrightarrow{AD}$ .

a) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B). Gọi M(x_M; y_M; z_M) là trung điểm của đoạn thẳng AB.

Ÿ Biểu diễn vectơ $\overrightarrow{OM}$ theo hai vectơ $\overrightarrow{OA}$   và $\overrightarrow{OB}$  .

Ÿ Tính tọa độ của điểm M theo tọa độ của các điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B).

Cho hình hộp ABCD.A'B'C'D', biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C'(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác  vuông góc với cả hai vectơ trong mỗi trường hợp sau:

a) $\overrightarrow{AC}$  và $\overrightarrow{B^{\text{'}}{D}^{\text{'}}}$ ;

b) Cho hai vectơ  $\overrightarrow{u}=\left(x_1;y_1;z_1\right)$và $\overrightarrow{v}=\left(x_2;y_2;z_2\right)$  không cùng phương.

Xét vectơ $\overrightarrow{w}=\left(y_1{z}_2-y_2{z}_1;z_1{x}_2-z_2{x}_1;x_1{y}_2-x_2{y}_1\right)$  .

Ÿ Tính $\overrightarrow{w}\cdot \overrightarrow{u},\overrightarrow{w}\cdot \overrightarrow{v}$ .

Ÿ Vectơ $\overrightarrow{w}$   có vuông góc với cả hai vectơ $\overrightarrow{u}$  và  hay không?

Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(2;-2;1\right),\overrightarrow{b}=\left(2;1;3\right)$  . Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{c}$  khác $\overrightarrow{0}$  vuông góc với cả hai vectơ  và .

Trong không gian với hệ tọa độ Oxyz, cho  $\overrightarrow{a}=\left(0;1;1\right)$và $\overrightarrow{b}=\left(-1;1;0\right)$  . Góc giữa hai vectơ $\overrightarrow{a}$  và $\overrightarrow{b}$  bằng:

A. 60°.

B. 120°.

C. 150°.

D. 30°.

Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a}=\left(2;3;-2\right)$   và $\overrightarrow{b}=\left(3;1;-1\right)$ . Tọa độ của vectơ $\overrightarrow{a}-\overrightarrow{b}$  là:

A. (1; – 2; 1).

B. (5; 4; – 3).

C. (– 1; 2; – 1).

D. (– 1; 2; – 3).