Hình thang cân ABCD (AB // CD) có , DB là tia phân giác của góc D. Tính các cạnh của hình thang, biết chu vi hình thang bằng 20cm.

Hình thang ABCD cân có AB // CD

⇒ $\angle$D = $\angle$C = ${60}^0$

DB là tia phân giác của góc D

⇒ $\angle$(ADB) = $\angle$(BDC)

$\angle$(ABD) = $\angle$(BDC) (hai góc so le trong)

Suy ra: $\angle$(ADB) = $\angle$(ABD)

⇒ $∆$ABD cân tại A ⇒ AB = AD (1)

Từ B kẻ đường thẳng song song với AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = ED, AD= BE (2)

$\angle$(BEC) = $\angle$(ADC) (đồng vị )

Suy ra: $\angle$(BEC) = $\angle$C = ${60}^0$

⇒$∆$ BEC đều ⇒ EC = BC (3)

AD = BC (tính chất hình thang cân) (4)

Từ (1), (2), (3) và (4) ⇒ AB = BC = AD = ED = EC

⇒ Chu vi hình thang bằng:

AB + BC + CD + AD = AB + BC + EC + ED + AD = 5AB

⇒AB = BC = AD = 20 : 5 = 4 (cm)

CD = CE + DE = 2 AB = 2.4 = 8 (cm)

Lý thuyết Hình thang cân

1. Khái niệm

Hình thang là tứ giác có hai cạnh đối song song.

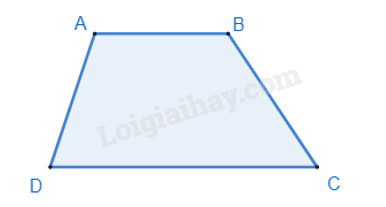
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

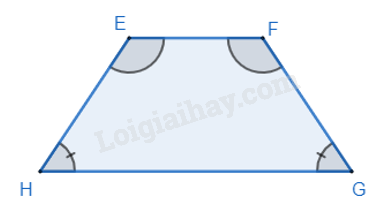
 2. Tính chất của hình thang cân

+ Hai cạnh bên bằng nhau.

+ Hai đường chéo bằng nhau.

Ví dụ:

 

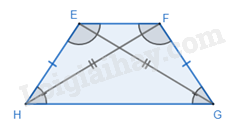
 Hình thang cân EFGH có hai cạnh bên EH = FG, hai đường chéo EG = FH.

3. Dấu hiệu nhận biết hình thang cân

- Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

- Hình thang có hai đường chéo bằng nhau là hình thang cân.

Bài tập liên quan: 

Hình thang cân ABCD (AB// CD) có $\angle$(A ) = ${70}^0$. Khẳng định nào dưới đây là đúng ?

A. $\angle$(C ) = ${110}^0$

B. $\angle$(B ) = ${110}^0$

C. $\angle$(C ) = ${70}^0$

D. $\angle$(D ) = ${70}^0$

Cách giải:

Chọn A. $\angle$(C ) = ${110}^0$

Ta có : $\angle$(A )+ $\angle$(D )=${180}^0$ ( hai góc trong cùng phía)

=>$\angle$(D )= ${180}^0$-$\angle$(A )= ${180}^0$- ${70}^0$ =${110}^0$

mà $\angle$(C )= $\angle$(D ) (tính chất hình thang cân ) =>$\angle$(C )= $\angle$(D )= ${110}^0$

Tham khảo thêm một số tài liệu liên quan:

Lý thuyết Hình thang cân (Cánh diều) | Lý thuyết Toán lớp 8

25 câu Trắc nghiệm Hình thang cân (Cánh diều) - Toán lớp 8