 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp giải:
Phương trình: cot x = m. Điều kiện: x ≠ kπ (k ∈ Z)
- Nếu m biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ cot x = cot α ⇔ x = α + kπ (k ∈ Z)
- Nếu m không biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ x = αrccot m + kπ (k ∈ Z)
* Mở rộng công thức nghiệm, với u(x) và v(x) là hai biểu thức của x.
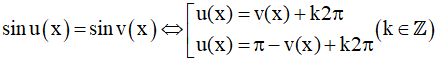
cos u(x) = cos v(x) ⇔ u(x) = 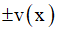 + k2π (k ∈ Z)
+ k2π (k ∈ Z)
tan u(x) = tan v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z)
cot u(x) = cot v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z)
Hướng dẫn giải:
Điều kiện , .
Vậy phương trình đã cho có nghiệm là , .
Bài tập liên quan:
Cho phương trình , m là tham số. Với giá trị nào của m thì phương trình trên vô nghiệm?
A. .
B. .
C. .
D. Không tồn tại giá trị của .
Cách giải:
Đáp án D
Tập giá trị nên với phương trình luôn có nghiệm.
Vậy không tồn tại giá trị m để phương trình vô nghiệm.
Tham khảo thêm một số tài liệu liên quan:
50 Bài tập Phương trình lượng giác cơ bản (có đáp án) - Toán 11
50 Bài tập Một số phương trình lượng giác thường gặp (có đáp án)- Toán 11
Cho phương trình , m là tham số. Với giá trị nào của m thì phương trình trên vô nghiệm?