Đường thẳng y = x - 1 cắt đồ thị hàm số y = (2x-1)/(x+1)...

Question

Đường thẳng y = x - 1 cắt đồ thị hàm số y=2x-1x+1 tại các điểm có tọa độ là

VietJack · Accepted Answer

Chọn C. Phương trình hoành độ giao điểm : Thế vào phương trình y = x - 1 được tung độ tương ứng 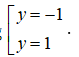Vậy đường thẳng cắt đồ thị tại hai điểm là: (0;-1), (2;1) Lý thuyết. + Cho hai đường thẳng d: y = ax + b và d’: y = a’x + b’ với a≠0 và a’≠0. Hai đường thẳng này có duy nhất một điểm chung khi chúng cắt nhau. Hai đường thẳng không có điểm chung khi chúng song song. Hai đường thẳng có vô số điểm chung khi chúng trùng nhau. + Muốn tìm tọa độ giao điểm hai đường thẳng ta làm như sau (d và d’ cắt nhau) Bước 1: Xét phương trình hoành độ giao điểm của d và d’. ax + b = a’x + b’ (1) Chú ý: + Phương trình (1) vô nghiệm thì d // d’. + Phương trình (1) luôn đúng với mọi giá trị x thì d và d’ trùng nhau. + Với a ≠ a’, phương trình (1) có nghiệm duy nhất. (1)⇔ax−a'x=−b+b' ⇔xa−a'=−b+b' ⇔x=−b+b'a−a' Ta chuyển qua bước 2 Bước 2: Thay x vừa tìm được vào d hoặc d’ để tính y Ví dụ thay x vào d ⇒y=a.−b+b'a−a'+b Bước 3: Kết luận tọa độ giao điểm. Xem thêm một số kiến thức liên quan: Lý thuyết Toán 12 Chương 1 (Kết nối tri thức): Ứng dụng đạo hàm đề khảo sát và vẽ đồ thị hàm số Tìm tọa độ giao điểm và góc giữa hai đường thẳng d1 và d2 trong mỗi trường hợp sau

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Đường thẳng $y = x - 1$ cắt đồ thị hàm số $y = \frac{2 x - 1}{x + 1}$ tại các điểm có tọa độ là

A. (0;2)

B. (-1;0); (2;1)

C. (0;-1); (2;1)

D. (1;2)

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Đồ thị hàm số $y = x^{3} - 3 x^{2} + 1$ cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị tham số m thỏa mãn là

Câu 2:

Cho hàm số $y = - x^{4} + 2 x^{2} + m$ . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là

Câu 3:

Cho hàm số $(C) : y = \frac{x}{x - 1}$ và đường thẳng $d : y = x + m .$ Tập tất cả các giá trị của tham số m sao cho (C) và d cắt nhau tại hai điểm phân biệt là

Câu 4:

Cho hàm số $y = - 2 x^{3} + 6 x^{2} - 5$ . Phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng

Câu 5:

Cho hàm số $y = (x - 2) (x^{2} + m x + m^{2} - 3)$ Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là

Câu 6:

Cho hàm số $y = 3 x - 4 x^{3}$ có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?

Câu 7:

Cho hàm số $(C) : y = x^{3} + 3 x^{2}$ . Phương trình tiếp tuyến của đồ thị (C) tại điểm M(1; 4) là

Đề thi liên quan

Câu hỏi mới nhất