Chứng minh rằng với mọi tam giác ABC, ta có:

$S_{ABC}=\frac{1}{2}\sqrt{{\overrightarrow{AB}}^2.{\overrightarrow{AC}}^2-{\left(\overrightarrow{AB}.\overrightarrow{AC}\right)}^2}.$

Cho tam giác ABC có BC = a, CA = b, AB = c. Hãy tính $\overrightarrow{AB}.\overrightarrow{AC}$ theo a, b, c.

Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có:

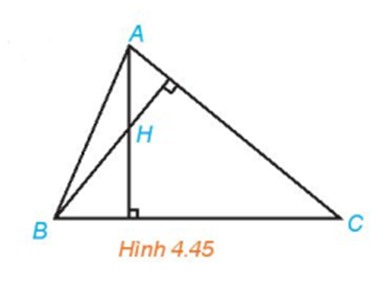
Cho tam giác ABC với A(-1;2), B(8;-1), C(8;8). Gọi H là trực tâm tam giác ABC.

a) Chứng minh rằng $\overrightarrow{AH}.\overrightarrow{BC}=\overrightarrow{0}$ và $\overrightarrow{BH}.\overrightarrow{CA}=\overrightarrow{0}.$

b) Tìm tọa độ của H.

c) Giải tam giác ABC.

Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(-4;1), B(2;4), C(2;-2).

a) Giải tam giác ABC.

b) Tìm tọa độ trực tâm H của tam giác ABC.

Tìm điều kiện của $\overrightarrow{u},\overrightarrow{v}$ để:

a) $\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|;$

b) $\overrightarrow{u}.\overrightarrow{v}=-\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|;$

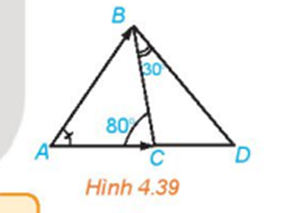
Trong Hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}$. Hãy tìm số đo các góc giữa $\overrightarrow{BC}$ và $\overrightarrow{BD}$, $\overrightarrow{DA}$ và $\overrightarrow{DB}$.

Cho ba vecto $\overrightarrow{u}\left(x_1;y_1\right),\overrightarrow{v}\left(x_2;y_2\right),\overrightarrow{w}\left(x_3;y_3\right).$ 

a) Tính $\overrightarrow{u}\left(\overrightarrow{v}+\overrightarrow{\text{w}}\right),\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{\text{w}}$ theo tọa độ các vecto $\overrightarrow{u},\overrightarrow{v},\overrightarrow{\text{w}}.$

b) So sánh $\overrightarrow{u}\left(\overrightarrow{v}+\overrightarrow{\text{w}}\right)$ và $\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{\text{w}}$.

c) So sánh $\overrightarrow{u}.\overrightarrow{v}$ và $\overrightarrow{v}.\overrightarrow{u}$.

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;2), B(-4;3). Gọi M(t;0) là một điểm thuộc trục hoành.

a) Tính $\overrightarrow{AM}.\overrightarrow{BM}$ theo t.

b) Tính t để $\widehat{AMB}={90}^0.$

Tính tích vô hướng và góc giữa hai vecto $\overrightarrow{u}\left(0;-5\right),\overrightarrow{v}\left(\sqrt{3};1\right)$.

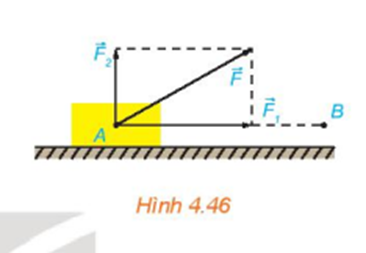
Một lực $\overrightarrow{F}$ không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng đều từ A đến B. Lực $\overrightarrow{F}$ được phân tích thành hai lực thành phần $\overrightarrow{F_1}$ và $\overrightarrow{F_2}\left(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}\right)$ 

a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực  (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực $\overrightarrow{F_1}$ và $\overrightarrow{F_2}.$

b) Giả sử các lực thành phần $\overrightarrow{F_1}$ và $\overrightarrow{F_2}.$ tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực  và lực $\overrightarrow{F_1}$

Cho hai vecto cùng phương $\overrightarrow{u}=\left(x;y\right)$ và $\overrightarrow{v}=\left(kx;ky\right).$ Hãy kiểm tra công thức $\overrightarrow{u}.\overrightarrow{v}=k\left(x^2+y^2\right)$ theo từng trường hợp sau:

a) $\overrightarrow{u}=\overrightarrow{0};$

b) $\overrightarrow{u}\ne \overrightarrow{0}$ và $k\ge 0;$

c) $\overrightarrow{u}\ne \overrightarrow{0}$ và k < 0.

Khi nào tích vô hướng của hai vecto $\overrightarrow{u},\overrightarrow{v}$ là một số dương? Là một số âm?

Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ trong mỗi trường hợp sau:

a) $\overrightarrow{a}\left(-3;1\right),\overrightarrow{b}\left(2;6\right);$

b) $\overrightarrow{a}\left(3;1\right),\overrightarrow{b}\left(2;4\right);$

c) $\overrightarrow{a}\left(-\sqrt{2};1\right),\overrightarrow{b}\left(2;-\sqrt{2}\right);$