Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác đó.
 Giải bởi Vietjack
Giải bởi Vietjack
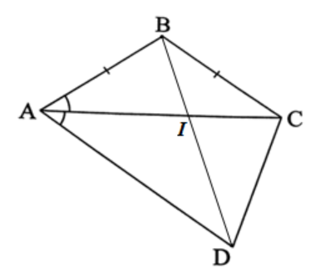
Vẽ tứ giác ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
Theo bất đẳng thức tam giác, ta có:
IA + IB > AB (trong tam giác IAB)
IB + IC > BC (trong tam giác IBC)
IC + ID > CD (trong tam giác ICD)
IA + ID > AD (trong tam giác IAD)
Suy ra 2(IA + IB + IC + ID) > AB + BC + CD + DA
Hay 2(AC + BD) > AB + BC + CD + DA
Vậy hay tổng độ dài hai đường chéo của một tứ giác lớn hơn nửa chu vi của tứ giác đó.
Cho tứ giác ABCD có AB = AD, CB = CD,
a) Chứng minh AC là đường trung trực của BD.
b) Tính số đo góc B và góc D.
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau tại I. Cho biết BC = 15 cm, CD = 24 cm và AD = 20 cm. Tính độ dài AB.
Cho tứ giác ABCD có Các tia phân giác của góc A và góc B cắt nhau tại I. Biết Tính số đo góc C và góc D.
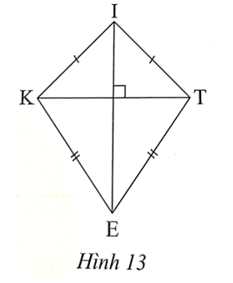
Bạn Hùng muốn làm một cái diều có dạng hình tứ giác KITE như Hình 13. Cho biết IK = IT, EK = ET. Tìm số đo các góc còn lại của tứ giác KITE.
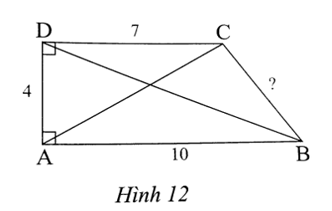
Cho tứ giác ABCD như Hình 12.
a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.
b) Cho biết góc B bằng 53°. Tìm số đo góc C.