Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ.

Tìm cực trị của các hàm số sau:

Xét một chất điểm chuyển động dọc theo trục Ox. Tọa độ của chất điểm tại thời điểm t được xác định bởi hàm số x(t) = t³ – 6t² + 9t với t ³ 0. Khi đó x'(t) là vận tốc của chất điểm tại thời điểm t, kí hiệu v(t); v'(t) là gia tốc chuyển động của chất điểm tại thời điểm t, kí hiệu a(t).

a) Tìm các hàm v(t) và a(t).

Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:

Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).

b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Chứng minh rằng hàm số $y=\frac{2x+1}{x-3}$ nghịch biến trên từng khoảng xác định của nó.

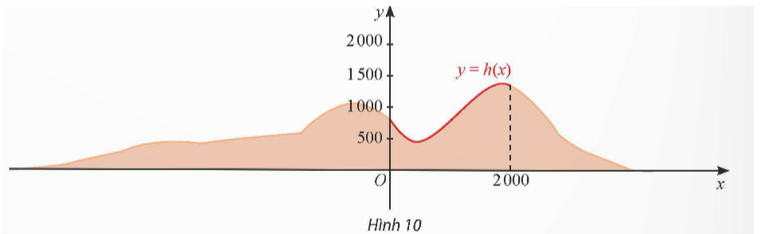
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y=h\left(x\right)=-\frac{1}{1320000}{x}^3+\frac{9}{3520}{x}^2-\frac{81}{44}x+840$ với 0 £ x £ 2000.

Tìm tọa độ các đỉnh của lát cắt dãy núi trên đọan [0; 2000].

(Theo: Tập bản đồ bài tập và bài thực hành Địa lí 8, Nhà xuất bản Giáo dục Việt Nam, 2011).

b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

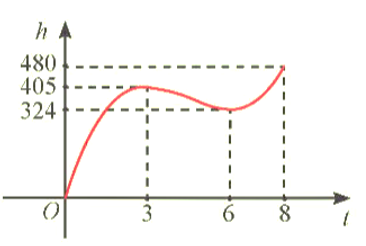
Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số h(t) = 6t³ – 81t² + 324t với 0 £ t £ 8.

Xét tính đơn điệu của các hàm số sau:

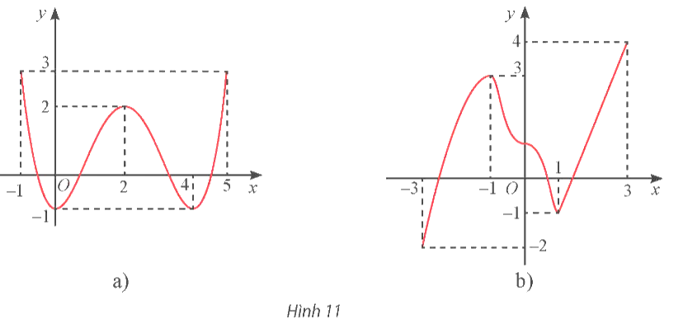
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.

Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:

Tìm cực trị của các hàm số sau:

Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức h(t) = 6t³ – 81t² + 324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào thì khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?