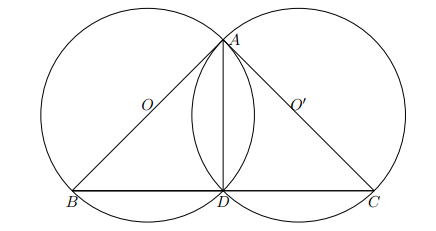
Cho tam giác ABC. Hai đường tròn đường kính AB và AC cắt nhau tại một điểm thứ hai là D.

a) Chứng minh rằng ba điểm B, D, C thẳng hàng.

b) Đường thẳng AC cắt đường tròn đường kính AB tại E, đường thẳng AB cắt đường tròn đường kính AC tại F. Chứng minh rằng ba đường thẳng AD, BE, CF cùng đi qua một điểm.

Cho đường tròn (O) và hai dây MA, MB vuông góc với nhau. Gọi I và K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI

a) Chứng minh ba điểm A, O, B thẳng hàng.

b) Chứng minh rằng P là tâm đường tròn nội tiếp của $∆\mathrm{MAB}$

c) Giả sử MA = 12 cm, MB = 16 cm, tính bán kính của đường tròn nội tiếp $∆\mathrm{MAB}$

Cho $∆\mathrm{ABC}$ có ba góc nhọn. Đường tròn (O) có đường kính BC cắt AB, AC tại D, E. Gọi I là giao điểm của BS và CD.

a) Chứng minh rằng $\mathrm{AI}\perp \mathrm{BC}$

b) Chứng minh rằng $\widehat{\mathrm{IAE}}=\widehat{\mathrm{IDE}}$

c) Cho $\widehat{\mathrm{BAC}}={60}^0$, chứng minh $∆\mathrm{DOE}$ là tam giác đều.

Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ một đường tròn (I) tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường kính AB tại D, đường tròn này cắt CA và CB tại các điểm thứ hai là M và N. Chứng minh rằng:

a) Ba điểm M, I, N thẳng hàng

b) $\mathrm{ID}\perp \mathrm{MN}$

c) Đường thẳng CD đi qua điểm cố định

d) Nêu cách dựng đường tròn (I) nói trên.

Cho $∆\mathrm{ABC}$ nội tiếp đường tròn (O). Tia phân giác góc A cắt đường tròn tại M.

a) Chứng minh rằng $∆\mathrm{BMC}$là tam giác cân.

b) Chứng minh rằng $\widehat{\mathrm{BMC}}=\widehat{\mathrm{ABC}}+\widehat{\mathrm{ACB}}$

c) Gọi D là giao điểm của AM và BC. Chứng minh rằng AB.AC = AD.AM

Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Gọi K là giao điểm của EB với đường tròn (O) và H là giao điểm của BD và AK.

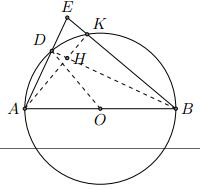
a) $∆$ABE là tam giác gì?

b) Chứng minh rằng EH vuông góc với AB.

c) Chứng minh rằng OD vuông góc với AK.

Cho đường tròn (O) và hai dây AB, CD bằng nhau cắt nhau tại M (điểm C nằm trên cung nhỏ AB, điểm B nằm trên cung nhỏ CD)

a) Chứng minh AC = DB

b) Chứng minh $∆\mathrm{MAC}=∆\mathrm{MDB}$

c) Tứ giác ACBD là hình gì? Chứng minh.

Cho $∆\mathrm{ABC}$ có ba góc nhọn nội tiếp đường tròn (O), đường cao AH. Kẻ đường kính AE.

a) Tính $\widehat{\mathrm{ACE}}$

b) Chứng minh rằng $\widehat{\mathrm{BAH}}=\widehat{\mathrm{OAC}}$

c) Gọi K là giao điểm của AH với đường tròn (O). Tứ giác BCEK là hình gì?

Cho nửa đường tròn (O) có đường kính AB và C là một điểm bên ngoài đường tròn. Nối CA, CB gặp đường tròn theo thứ tự ở M, N. Gọi H là giao điểm của BM và AN.

a) Chứng minh rằng $\mathrm{AH}\perp \mathrm{AB}$

b) Cho $\widehat{\mathrm{ACB}}={60}^0$, chứng minh $∆\mathrm{OMN}$ là tam giác đều.

Cho tam giác ABC. Đường tròn (I) nội tiếp tam giác tiếp xúc với BC, AC, BA theo thứ tự tại D, E, F. Cho biết $\widehat{\mathrm{BAC}}=\widehat{\mathrm{EDF}}$. Tính số đo của góc $\widehat{\mathrm{BAC}}$.

Cho nửa đường tròn đường kính AB. Gọi O là điểm chính giữa của nửa đường tròn và M là một điểm bất kì của nửa đường tròn đó. Tia AM cắt đường tròn (O; OA) tại điểm thứ hai là N. Chứng minh rằng MN = MB.

Cho nửa đường tròn đường kính AB, K là điểm chính giữa cung AB. Vẽ bán kính OC sao cho $\widehat{\mathrm{BOC}}={60}^0$

a) Gọi M là giao điểm của AC và OK. Chứng minh rằng MO = MC

b) Cho AB = 2R, tính MC theo R.

Hai đường tròn (O; R) và (O’; r) cắt nhau tại A và B. Từ A vẽ đường kính AOC và AO’D

a) Chứng minh ba điểm B, C, D thẳng hàng và AB vuông góc với CD.

b) Biết R$\ge \mathrm{r}$ và CD = a, hãy tính BC và BD.

Cho đường tròn (O) và (O’) bằng nhau, cắt nhau tại A và B. Qua B vẽ một cát tuyến cắt đường tròn (O) và (O’) lần lượt tại C và D.

a) Chứng minh AC = AD.

b) Tìm quỹ tích trung điểm M của CD khi cát tuyến CBD quay quanh B.

Cho một đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M vẽ một cát tuyến cắt đường tròn ở A và B. Chứng minh rằng tích MA.MB không phụ thuộc vào vị trí của cát tuyến.