Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
 Giải bởi Vietjack
Giải bởi Vietjack
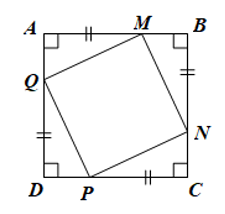

Sử dụng một trong hai cách sau:
1. Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Tổng quát: ABCD là hình vuông ⇔
Nhận xét:
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
+ Hình vuông là hình thoi có bốn góc vuông.
+ Hình vuông vừa là hình chữ nhật vừa là hình thoi.
2. Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết hình vuông
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
Xem thêm kiến thức liên quan
Lý thuyết Hình thoi và hình vuông (Kết nối tri thức) hay, chi tiết | Lý thuyết Toán lớp 8
20 câu Trắc nghiệm Hình thoi và hình vuông (Kết nối tri thức) có đáp án - Toán lớp 8
Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:
a) ΔABM = ΔBCN;
Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a) ΔIAM = ΔICN;
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a) và tam giác ACM là tam giác vuông;
Cho hình bình hành MNPQ có các góc khác 90°, MP cắt NQ tại I. Khi đó
A. IM = IN.
B. IM = IP.
C. IM = IQ.
D. IM = MP.
Cho hình chữ nhật ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi.
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao cho AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Màn hình một chiếc ti vi có dạng hình chữ nhật với kích thước màn hình ti vi được tính bằng độ dài đường chéo của màn hình (đơn vị: inch, trong đó 1 inch = 2,54 cm). Người ta đưa ra công thức tính khoảng cách an toàn khi xem ti vi để giúp khách chọn được chiếc ti vi phù hợp với căn phòng hàng của mình như sau:
Khoảng cách tối thiểu = 5,08 . d (cm);
Khoảng cách tối đa = 7,62 . d (cm).
Trong đó, d là kích thước màn hình ti vi tính theo inch.
Với một chiếc ti vi có chiều dài màn hình là 74,7 cm; chiều rộng màn hình là 32 cm:
a) Kích thước màn hình của chiếc ti vi đó là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?