Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng
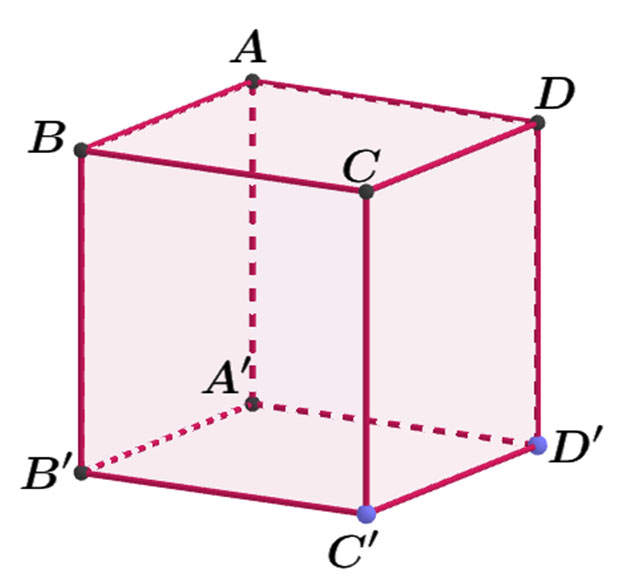
A. 2a;
B.
C. 3a;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng
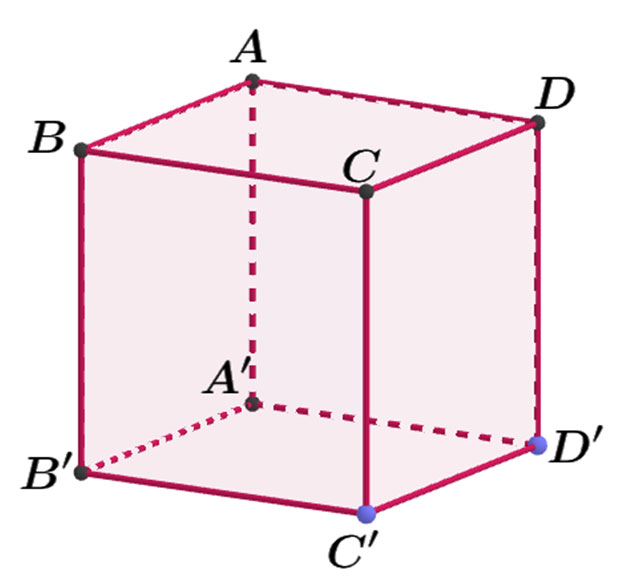
![]()
BD // (A'B'C'D') suy ra d (BD, A'C') = d (BD, (A'B'C'D'))
= d (B, (A'B'C'D')) = BB' = 3a.
Phương pháp giải Khoảng cách giữa hai đường thẳng chéo nhau
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta dựng đoạn vuông góc chung MN của a và b. Khi đó d(a, b) = MN. Sau đây là một số cách dựng đoạn vuông góc chung thường dùng:
Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng và song song với '. Khi đó d(, ') = d(', (α)).
Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
- Trường hợp 1: và ' vừa chéo nhau vừa vuông góc với nhau.
Bước 1: Chọn mặt phẳng (α) chứa ' và vuông góc với tại I.
Bước 2: Trong mặt phẳng (α) kẻ IJ '.
Khi đó IJ là đoạn vuông góc chung và d(, ') = IJ.
- Trường hợp 2: và ' vừa chéo nhau và không vuông góc với nhau.
Bước 1: Chọn mặt phẳng (α) chứa ' và song song với .
Bước 2: Dựng d là hình chiếu vuông góc của xuống (α) bằng cách lấy điểm M dựng đoạn MN (α), lúc đó d là đường thẳng đi qua N và song song với .
Bước 3: Gọi H = d ', dựng HK // MN.
Khi đó HK là đoạn vuông góc chung và d(, ') = HK = MN.
Hoặc
Bước 1: Chọn mặt phẳng (α) tại I.
Bước 2: Tìm hình chiếu d của ' xuống mặt phẳng (α).
Bước 3: Trong mặt phẳng (α), dựng IJ d, từ J dựng đường thẳng song song với cắt ' tại H, từ H dựng HM // IJ.
Khi đó HM là đoạn vuông góc chung và d(, ') = HM = IJ.
Bài tập có liên quan:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, BC = 2, AA' = 2. Khoảng cách giữa hai đường thẳng AD' và DC' bằng? (tham khảo hình)
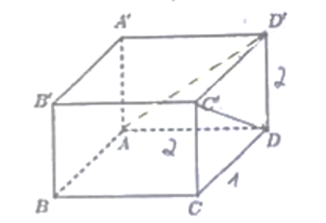
Bài giải
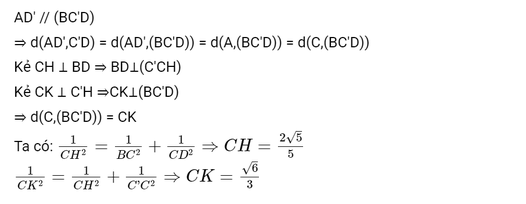
Tham khảo thêm một số tài liệu liên quan:
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (5b - 1)(a.2b - 5) < 0?
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Cho tam giác OIM vuông tại I có OI = 3 và IM = 4. Khi quay tam giác OIM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành hình nón có độ dài đường sinh bằng
Trong không gian Oxyz, cho điểm A(0; -3; 2) và mặt phẳng (P): 2x - y + 3z + 5 = 0. Mặt phẳng đi qua A và song song với (P) có phương trình là
Trong không gian Oxyz, cho ba điểm A(1; 2; -1), B(3; 0; 1) và C(2; 2; -2). Đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có phương trình là
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình:
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z = 2 - 7i có tọa độ là
Cho hình trụ có chiều cao h = 1 và bán kính r = 2. Diện tích xung quanh của hình trụ đã cho bằng
Biết F (x) và G (x) là hai nguyên hàm của hàm số f (x) trên ℝ và . Gọi S là diện tích hình phẳng giới hạn bỡi các đường y = F (x), y = G (x), x = 0 và x = 5. Khi S = 20 thì a bằng?