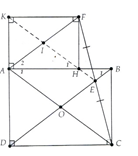
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật;
b) AF song song với BD;
c) Ba điểm E, H, K thẳng hàng
 Giải bởi Vietjack
Giải bởi Vietjack
a)
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
Cách chứng minh tứ giác là hình chữ nhật:
Nhận dạng hình chữ nhật theo ba cách sau:
Cách 1: Chứng minh tứ giác có ba góc vuông.
Cách 2: Chứng minh tứ giác là một hình thang cân có thêm một góc vuông.
Cách 3: Chứng minh tứ giác là hình bình hành có thêm một góc vuông hoặc hai đường chéo bằng nhau.
Bài tập liên quan:
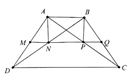
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng.
b) Chứng minh tứ giác ABPN là hình thang cân.
c) Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
Cách giải:
a) HS tự chứng minh hình thang ABPN có hai đường chéo bằng nhau là hình thang cân.
c) Cần thêm điều kiện NP = AB suy ra DC = 3AB
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Hình chữ nhật (Kết nối tri thức) | Lý thuyết Toán lớp 8
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì ?
b) Chứng minh rằng CH ^ AB.
c) Chứng minh tam giác PIQ cân.
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi M, N, P, Q lần lượt là trung điểm các đoạn thẳng AD, BD, AC, BC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng.
b) Chứng minh tứ giác ABPN là hình thang cân.
c) Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.
b) Chứng minh HG = GK = KE.
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật ?
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M Î AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, và K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:
a)
b) Chu vi DIHK bằng nửa chu vi DABC.
Cho hình thang vuông ABCD () có các điểm E và F thuộc cạnh AD sao cho AE = DF và . Chứng minh
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?