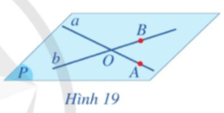
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với mặt phẳng (SAB).
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).
Giải bởi Vietjack
Phương pháp giải:
a. Tìm giao điểm giữa đường thẳng và mặt phẳng:
Muốn tìm giao điểm của đường thẳng d và mặt phẳng (P), có hai cách làm như sau:
* Cách 1:
+ Những bài đơn giản, có sẵn một mặt phẳng (Q) chứa đường thẳng d và một đường thẳng a nào đó thuộc mặt phẳng (P)
+ Trong mp( Q), 2 đường thẳng a và d cắt nhau tai điểm A. Khi đó điểm A chính là giao điểm của đường thẳng d và mp(P)
* Cách 2: Chọn mặt phẳng phụ:
+ Tìm một mặt phẳng (Q) chứa đường thẳng d, sao cho dễ dàng tìm giao tuyến của mp (Q) với mp (P)
+ Tìm giao tuyến của mp(P) và (Q) - gọi là đường thẳng d.
+ Tìm giao điểm của đường thẳng a và đường thẳng d - gọi là điểm A
Khi đó: điểm A chính là giao điểm của đường thẳng d và mp (P)
b. Tìm giao điểm giữa mặt phẳng và mặt phẳng:
Muốn tìm giao tuyến của hai mặt phẳng: ta tìm hai điểm chung thuộc cả hai mặt phẳng. Nối hai điểm chung đó được giao tuyến cần tìm.
Về dạng này điểm chung thứ nhất thường dễ tìm. Điểm chung còn lại các bạn phải tìm hai đường thẳng lần lượt thuộc hai mặt phẳng, đồng thời chúng lại thuộc mặt phẳng thứ ba và chúng không song song. Giao điểm của hai đường thẳng đó là điểm chung thứ hai.
Chú ý: Giao tuyến là đường thẳng chung của hai mặt phẳng, có nghĩa là giao tuyến là đường thẳng vừa thuộc mặt phẳng này vừa thuộc mặt phẳng kia.
Lời giải
a) Trong mặt phẳng (ABCD) ta có: gọi giao điểm của AB và CD là N.
Mà AB ⊂ (SAB)
Do đó CD ∩ (SAB) = {N}.
b) Ta có: AB ∩ CD = {N};
AB ⊂ (SAB);
CD ⊂ (SCD)
Do đó N là giao điểm của (SAB) và (SCD).
Lại có: S ∈ (SAB) và S ∈ (SCD).
Nên S là giao điểm của (SAB) và (SCD).
Vì vậy (SAB) ∩ (SCD) = SN.
c) Ta có: C ∈ (SBC) và C ∈ (MCD).
Do đó C là giao điểm của (SBC) và (MCD).
Trong mặt phẳng (SAB), gọi Q là giao điểm của MN và SB.
Mà MN ⊂ (MCD) và SB ⊂ (SBC)
Suy ra Q là giao điểm của (SBC) và (MCD).
Vì vậy (SBC) ∩ (MCD) = CQ.
Bài tập liên quan:
Sân vận động Old Trafford (Hình 2) ở thành phố Manchester, có biệt danh là “Nhà hát của những giấc mơ”, với sức chứa 75 635 người, là sân vận động lớn thứ hai ở Vương quốc Anh.
Quan sát Hình 2 và cho biết mặt sân vận động thường được làm phẳng hay cong.
Cách giải:
Mặt của sân vận động là mặt phẳng.
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Đường thẳng và mặt phẳng trong không gian (Cánh diều 2024) hay, chi tiết | Toán lớp 11
Sách bài tập Toán 11 Bài 1 (Cánh diều): Đường thẳng và mặt phằng trong không gian
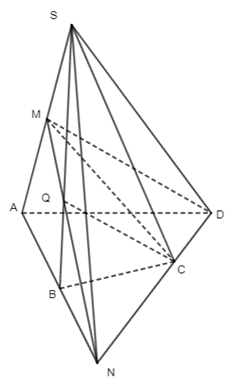
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA = 2MS, NS = 2NC.
a) Xác định giao điểm của MN với mặt phẳng (ABC).
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB.
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC).
Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.
a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).
b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: \(\frac{{GM}}{{GA}} = \frac{{GN}}{{GB}} = \frac{1}{3}\).
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và \(\frac{{GP}}{{GC}} = \frac{{GQ}}{{GD}} = \frac{1}{3}\).
Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho \(\frac{{AM}}{{AB}} = \frac{1}{3},\frac{{AN}}{{AD}} = \frac{2}{3},\frac{{BP}}{{BC}} = \frac{3}{4}\).
a) Xác định E, F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP).
b) Chứng minh rằng các đường thẳng NE, PF và CD cùng đi qua một điểm.
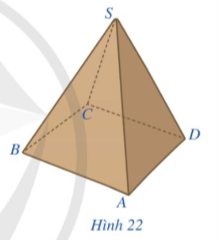
Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều S.ABCD. Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng (ABCD) hay không?
b) Mỗi mặt phẳng của hộp quà lưu niệm có dạng hình gì?
Hình 25 là hình ảnh của khối rubik tam giác (Pyraminx). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?
Sân vận động Old Trafford (Hình 2) ở thành phố Manchester, có biệt danh là “Nhà hát của những giấc mơ”, với sức chứa 75 635 người, là sân vận động lớn thứ hai ở Vương quốc Anh.
Quan sát Hình 2 và cho biết mặt sân vận động thường được làm phẳng hay cong.
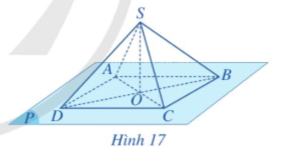
Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19).
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
