Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a. Cạnh bên SA vuông góc với đáy, góc giữa SD với đáy bằng . Tính khoảng cách d từ điểm C đến mặt phẳng (SBD) theo a.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
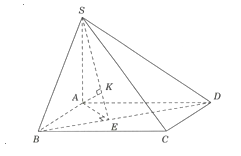
Xác định và .
Ta có .
Kẻ và kẻ .
Khi đó .
Tam giác vuông BAD, có .
Tam giác vuông SAE, có .
Vậy .
Phương pháp giải
Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)
Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)
Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK
Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP
Hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác vuông tại , đường cao (hình vẽ). Khi đó ta có các hệ thức sau:
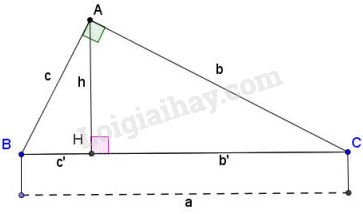
+) và hay và (1)
+) hay (2)
+) hay (3)
+) hay (4).
+) (Định lí Pitago).
Bài tập liên quan:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, , SA = a. Tính khoảng cách từ trung điểm I của SC đến (SBD).
A.
B.
C.
D.
Cách giải:
Đáp án B.
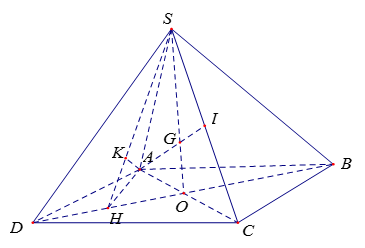
Kẻ và AK⊥SH
Ta có và
Ta có:
vuông
vuông =>
Gọi O
Tham khảo thêm một số tài liệu liên quan:
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;3), B(-1;0;1). Trọng tâm G của tam giác OAB có tọa độ là
Cho hình lập phương ABCD.EFGH. Tính tỉ số k giữa thể tích khối trụ ngoại tiếp và thể tích khối trụ nội tiếp hình lập phương đã cho.
Có bao nhiêu số có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?
Bất phương trình nghiệm đúng với mọi khi và chỉ khi
Cho khối nón có độ dài đường sinh bằng đường kính đáy bằng a. Thể tích của khối nón là

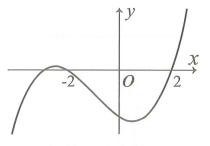
Hàm số đồng biến trên khoảng nào dưới đây?
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh , . Hai mặt bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính theo a thể tích V của khối chóp S.ABCD.