Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$  thỏa mãn $\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1$  và hai vectơ $\overrightarrow{u}=\frac{2}{5}\overrightarrow{a}-3\overrightarrow{b}$ và $\overrightarrow{v}=\overrightarrow{a}+\overrightarrow{b}$  vuông góc với nhau. Xác định góc $\alpha$ giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ .

Đáp án đúng là: B

Ta có: $\overrightarrow{u}\perp \overrightarrow{v}\Rightarrow \overrightarrow{u}.\overrightarrow{v}=0\iff \left(\frac{2}{5}\overrightarrow{a}-3\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=0\iff \frac{2}{5}{\overrightarrow{a}}^2-\frac{13}{5}\overrightarrow{a}\overrightarrow{b}-3{\overrightarrow{b}}^2=0$

 $\stackrel{\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1}{\to }\overrightarrow{a}\overrightarrow{b}=-1.$

Suy ra  $cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=-1\Rightarrow \left(\overrightarrow{a},\overrightarrow{b}\right)={180}^0.$

Lý thuyết Vecto

Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không $\overrightarrow{u}$ và $\overrightarrow{v}$ là một số, kí hiệu là $\overrightarrow{u}$.$\overrightarrow{v}$, được xác định bởi công thức sau:

$\overrightarrow{u}$. $\overrightarrow{v}$ = |$\overrightarrow{u}$|.|$\overrightarrow{v}$|.cos($\overrightarrow{u}$, $\overrightarrow{v}$)

Chú ý:

+) $\overrightarrow{u}$ ⊥ $\overrightarrow{v}$ ⇔ $\overrightarrow{u}$. $\overrightarrow{v}$ = 0.

+) $\overrightarrow{u}$. $\overrightarrow{u}$ còn được viết là ${\overrightarrow{u}}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{u}$.

Ta có ${\overrightarrow{u}}^2=\left|\overrightarrow{u}\right|.\left|\overrightarrow{u}\right|.\cos 0°={\left(\overrightarrow{u}\right)}^2$.

(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)

Hiệu của hai vectơ

– Vectơ có cùng độ dài và ngược hướng với vectơ $\overrightarrow{a}$ được gọi là vectơ đối của vectơ $\overrightarrow{a}$. Vectơ đối của vectơ $\overrightarrow{a}$ kí hiệu là –$\overrightarrow{a}$.

– Vectơ được coi là vectơ đối của chính nó.

– Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng $\overrightarrow{0}$.

– Vectơ $\overrightarrow{a}$+ (–$\overrightarrow{b}$) được gọi là hiệu của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ và được kí hiệu là $\overrightarrow{a}$– $\overrightarrow{b}$. Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

– Nếu $\overrightarrow{b}$+ $\overrightarrow{c}$= $\overrightarrow{a}$ thì $\overrightarrow{a}$– $\overrightarrow{b}$ = $\overrightarrow{a}$+ (–$\overrightarrow{b}$) = $\overrightarrow{c}$ + $\overrightarrow{b}$+ (–$\overrightarrow{b}$) = $\overrightarrow{c}$+ $\overrightarrow{0}$ = $\overrightarrow{c}$.

– Quy tắc hiệu: Với ba điểm O, M, N, ta có $\overrightarrow{MN}=\overrightarrow{MO}+\overrightarrow{ON}=\left(-\overrightarrow{OM}\right)+\overrightarrow{ON}=\overrightarrow{ON}-\overrightarrow{OM}$.

Phương pháp giải tính góc giữa hai vecto

Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ

Định nghĩa góc giữa hai vectơ: Cho hai vectơ  đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .

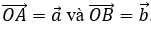
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ.

Sử dụng công thức sau:

Cho hai vectơ 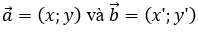. Khi đó

Chú ý: Góc giữa hai vectơ thuộc [0°;180°]

Bài tập liên quan: 

Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho $3\overrightarrow{AM}=2\overrightarrow{AB}$ và $3\overrightarrow{DN}=2\overrightarrow{DC}.$  Tính vectơ $\overrightarrow{MN}$  theo hai vectơ 

A. $\overrightarrow{MN}=\frac{1}{3}\overrightarrow{AD}+\frac{1}{3}\overrightarrow{BC};$

B. $\overrightarrow{MN}=\frac{1}{3}\overrightarrow{AD}-\frac{2}{3}\overrightarrow{BC};$

C. $\overrightarrow{MN}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC};$

D. $\overrightarrow{MN}=\frac{2}{3}\overrightarrow{AD}+\frac{1}{3}\overrightarrow{BC}.$

Cách giải:

Đáp án đúng là: C

Ta có : $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}$  và  $\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.$

Suy ra $3\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}+2\left(\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\right)$

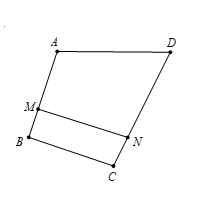
   $=\left(\overrightarrow{MA}+2\overrightarrow{MB}\right)+\overrightarrow{AD}+2\overrightarrow{BC}+\left(\overrightarrow{DN}+2\overrightarrow{CN}\right).$

Theo bài ra, ta có: $\overrightarrow{MA}+2\overrightarrow{MB}=\overrightarrow{0}$ và $\overrightarrow{DN}+2\overrightarrow{CN}=\overrightarrow{0}.$  Thật vậy:

$3\overrightarrow{AM}=2\overrightarrow{AB}\iff 3\overrightarrow{AM}=2\left(\overrightarrow{AM}+\overrightarrow{MB}\right)$

$\iff 3\overrightarrow{AM}=2\overrightarrow{AM}+2\overrightarrow{MB}$

$\iff \overrightarrow{AM}=2\overrightarrow{MB}$

$\iff 2\overrightarrow{MB}-\overrightarrow{AM}=0$

$\iff 2\overrightarrow{MB}+\overrightarrow{MA}=0$

$3\overrightarrow{DN}=2\overrightarrow{DC}\iff 3\overrightarrow{DN}=2(\overrightarrow{DN}+\overrightarrow{NC})$

$\iff 3\overrightarrow{DN}=2\overrightarrow{DN}+2\overrightarrow{NC}$

$\iff \overrightarrow{DN}=2\overrightarrow{NC}$

$\iff \overrightarrow{DN}-2\overrightarrow{NC}=0$

$\iff \overrightarrow{DN}+2\overrightarrow{CN}=0$

Vậy $3\overrightarrow{MN}=\overrightarrow{AD}+2\overrightarrow{BC}\iff \overrightarrow{MN}=\frac{1}{3}\overrightarrow{AD}+\frac{2}{3}\overrightarrow{BC}.$

Tham khảo thêm một số tài liệu liên quan:

Lý thuyết Chương 4: Vecto (Kết nối tri thức) | Toán lớp 10

30 câu Trắc nghiệm Chương 4: Vectơ (Kết nối tri thức) – Toán lớp 10