Cho góc α với cosα = . Tính giá trị của biểu thức A = 2sin2α + 5cos2α .
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có A = 2sin2α + 5cos2α
= 2sin2α + 2cos2α + 3cos2α
= 2(cos2α + sin2α ) + 3cos2α
= 2 . 1 + 3. = 2 + 3. = .
Vậy A = .
Phương pháp giải
* Phương pháp: Để tínhTính giá trị biểu thức liên quan đến giá trị lượng giác ta sử dụng các công thức lượng giác để biến đổi biểu thức lượng giác nhằm triệt tiêu các giá trị lượng giác không đặc biệt hoặc biến đổi biểu thức lượng giác về dạng chỉ xuất hiện giá trị đã cho của giả thiết để tính.
* Các công thức thường sử dụng:
* Các hệ thức lượng giác cơ bản:
√ sin2 α + cos2 α = 1;
√ (α≠π2+kπ, k ∈ℤ);
√ (α ≠ kπ , k ∈ ℤ);
√ tanα⋅cotα=1(, k ∈ ℤ).
√ Giá trị lượng giác của các góc liên quan đặc biệt:
√ Góc đối nhau (α và – α): cos (– α) = cos α; sin (– α) = – sin α;
tan (– α) = – tan α; cot (– α) = – cot α.
√ Góc bù nhau (α và π – α): sin (π – α) = sin α; cos (π – α) = – cos α;
tan (π – α) = – tan α; cot (π – α) = – cot α.
√ Góc phụ nhau (α và π2 – α): sin = cos α; cos = sin α;
tan = cot α; cot = tan α.
Góc hơn kém nhau π (α và π + α): sin (π + α) = –sin α; cos (π + α) = –cos α;
tan (π + α) = tan α; cot (π + α) = cot α.
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180 (Kết nối tri thức) | Toán lớp 10
20 câu Trắc nghiệm Giá trị lượng giác của 1 góc từ 0° đến 180° (Kết nối tri thức) – Toán lớp 10
Cho biết sin30° = ; sin60° = ; tan45° = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30° + sin150° + tan135°.
Cho biết sinα = , tìm góc α (0° ≤ α ≤ 180°) bằng cách vẽ nửa đường tròn đơn vị.
Cho tam giác ABC. Chứng minh rằng:
a) sinA = sin(B + C);
b) cosA = – cos(B + C).
Tính
A = sin150° + tan135° + cot45°;
B = 2cos30° – 3tan150° + cot135°.
Tìm góc α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) sinα = ;
b) cosα = ;
c) tanα = – 1;
d) cotα = .
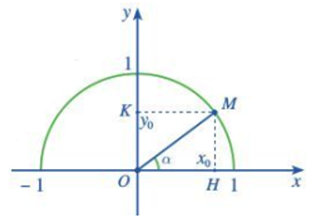
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho . Giả sử điểm M có tọa độ (x0; y0). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
sinα = y0; cosα = x0 ; tanα = ; cotα = .
Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:
a) Tính: sin168°45'33"; cos17°22'35"; tan156°26'39"; cot 56°36'42".
b) Tìm α (0° ≤ α ≤ 180°) trong các trường hợp sau:
i) sinα = 0,862;
ii) cosα = – 0,567;
iii) tanα = 0,334.
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:
a) cos2α + sin2α = 1;
b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) 1 + tan2α = (α ≠ 90°);
d) 1 + cot2 α = (0° < α < 180°).
a) Tính cos80°43'51"; tan147°12'25''; cot99°9'19".
b) Tìm α (0° ≤ α ≤ 180°), biết cosα = – 0,723.
Tìm α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) cosα = ;
b) sinα = 0;
c) tanα = 1;
d) cotα không xác định.
Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?