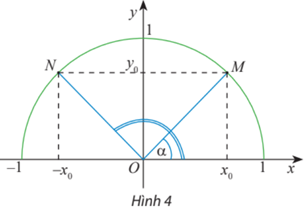
Cho biết sinα = , tìm góc α (0° ≤ α ≤ 180°) bằng cách vẽ nửa đường tròn đơn vị.
 Giải bởi Vietjack
Giải bởi Vietjack
Trên trục Oy của nửa đường tròn đơn vị lấy điểm .
Từ điểm H kẻ đường thẳng song song với trục Ox, cắt nửa đường tròn tại hai điểm M và M’.
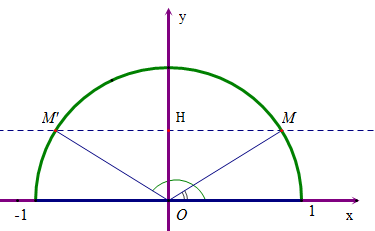
Ta có góc α cần tìm là : và .
Với α = và sinα = ⇒ α = 30°.
Mặt khác sin30° = sin(180° – 30°), tức là sin30° = sin150°.
Suy ra .
Vậy α = 30° hoặc α = 150°.
Cho góc α với cosα = . Tính giá trị của biểu thức A = 2sin2α + 5cos2α .
Cho biết sin30° = ; sin60° = ; tan45° = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30° + sin150° + tan135°.
Cho tam giác ABC. Chứng minh rằng:
a) sinA = sin(B + C);
b) cosA = – cos(B + C).
Tính
A = sin150° + tan135° + cot45°;
B = 2cos30° – 3tan150° + cot135°.
Tìm góc α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) sinα = ;
b) cosα = ;
c) tanα = – 1;
d) cotα = .
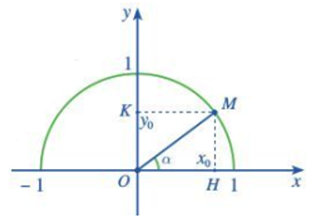
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn α, lấy điểm M trên nửa đường tròn đơn vị sao cho . Giả sử điểm M có tọa độ (x0; y0). Áp dụng cách tính tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
sinα = y0; cosα = x0 ; tanα = ; cotα = .
Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:
a) Tính: sin168°45'33"; cos17°22'35"; tan156°26'39"; cot 56°36'42".
b) Tìm α (0° ≤ α ≤ 180°) trong các trường hợp sau:
i) sinα = 0,862;
ii) cosα = – 0,567;
iii) tanα = 0,334.
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:
a) cos2α + sin2α = 1;
b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) 1 + tan2α = (α ≠ 90°);
d) 1 + cot2 α = (0° < α < 180°).
a) Tính cos80°43'51"; tan147°12'25''; cot99°9'19".
b) Tìm α (0° ≤ α ≤ 180°), biết cosα = – 0,723.
Tìm α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:
a) cosα = ;
b) sinα = 0;
c) tanα = 1;
d) cotα không xác định.
Làm thế nào để mở rộng khái niệm tỉ số lượng giác của góc nhọn cho các góc từ 0° đến 180°?