Cho góc lượng giác (Ou, Ov) có số đo là , góc lượng giác (Ou, Ow) có số đo là . Số đo của góc lượng giác (Ov, Ow) là
A. + k2π (k ∈ ℤ);
B. + k2π (k ∈ ℤ);
C. + k2π (k ∈ ℤ);
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Theo hệ thức Chasles, ta có:
sđ (Ov, Ow) = sđ (Ou, Ow) – sđ (Ou, Ov) + k2π = – + k2π = + k2π (k ∈ ℤ).
Góc lượng giác
a) Khái niệm góc lượng giác và số đo của góc lượng giác
– Trong mặt phẳng, cho hai tia Ou, Ov. Xét tia Om cùng nằm trong mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou, tia cuối Ov và kí hiệu là (Ou, Ov).
– Góc lượng giác (Ou, Ov) chỉ được xác định khi ta biết được chuyển động quay của tia Om từ tia đầu Ou đến tia cuối Ov (H.1.3). Ta quy ước: Chiều quay ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.
Khi đó, nếu tia Om quay theo chiều dương đúng một vòng ta nói tia Om quay góc 360°, quay đúng 2 vòng ta nói nó quay góc 720°; quay theo chiều âm nửa vòng ta nói nó quay góc –180°, quay theo chiều âm 1,5 vòng ta nói nó quay góc –1,5.360° = –540°, …
Khi tia Om quay góc α° thì ta nói góc lượng giác mà tia đó quét nên có số đo α°. Số đo của góc lượng giác có tia đầu Ou, tia cuối Ov được kí hiệu là sđ (Ou, Ov).
– Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của nó.
Chú ý: Cho hai tia Ou, Ov thì có vô số góc lượng giác tia đầu Ou, tia cuối Ov. Mỗi góc lượng giác như thế đều kí hiệu là (Ou, Ov). Số đo của các góc lượng giác này sai khác nhau một bội nguyên của 360°.
b) Hệ thức Chasles
Với ba tia Ou, Ov, Ow bất kì, ta có:
sđ (Ou, Ov) + sđ (Ov, Ow) = sđ (Ou, Ow) + k360° (k ∈ ℤ).
Nhận xét: Từ hệ thức Chasles, ta suy ra:
Với ba tia tùy ý Ox, Ou, Ov ta có:
sđ (Ou, Ov) = sđ (Ox, Ov) – sđ (Ox, Ou) + k360° (k ∈ ℤ).
Xem thêm một số kiến thức liên quan:
20 Bài tập Góc lượng giác. Giá trị lượng giác của góc lượng giác (sách mới) có đáp án – Toán 11
Cho góc lượng giác (OA, OB) có số đo bằng . Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
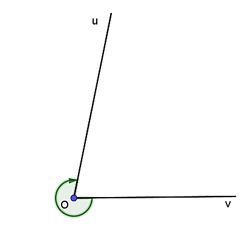
Cho góc hình học uOv = 75°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
Các góc lượng giác (Ox, Ou) và (Ox, Ov) có số đo lần lượt là –270° và 135°. Số đo của góc lượng giác (Ou, Ov) là
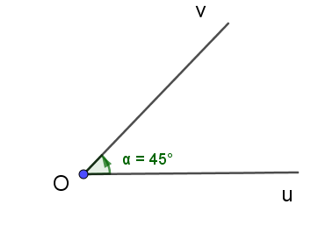
Cho góc hình học uOv = 45°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình vẽ sau:
Cho góc lượng giác (OA, OB) có số đo 395°. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác (OA, OB)?
Công thức biểu thị số đo của các góc lượng giác có cùng tia đầu và tia cuối với góc lượng giác có số đo bằng 120° là
Cho góc lượng giác (Ou, Ov) có số đo là , góc lượng giác (Ou, Ow) có số đo là . Tìm số đo của góc lượng giác (Ov, Ow) biết rằng 4π < sđ (Ov, Ow) < 6π.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 30 phút, kim phút quét một góc lượng giác bằng