Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. các đường thẳng CN và DN lần lượt cắt đường thẳng AB tại E và F. Tiếp tuyến của đường tròn tại N cắt đường thẳng AI tại I. Chứng minh rằng:

a) Các tam giác $∆\mathrm{INE}$ và $∆\mathrm{INF}$ là tam giác cân.

b) AI = $\frac{1}{2}$(AE + AF)

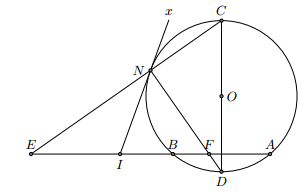
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD. Vẽ dây BM vuông góc với tia phân giác của góc BAC, dây này cắt CD tại E. Chứng minh rằng:

a) BM là tia phân giác của góc CBD

b) ${\mathrm{MD}}^2$ = ME.MB

Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Lấy điểm M thuộc tia đối của tia BC. Gọi I là giao điểm của MA với đường tròn. Chứng minh rằng:

a) $\widehat{\mathrm{AMC}}=\widehat{\mathrm{ACI}}$

b) AM.AI = ${\mathrm{AC}}^2$

Từ một điểm M ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.

Cho đường tròn (O) đường kính AB, cung CD = ${80}^0$ nằm cùng phía đối với AB (D thuộc cung BC). Gọi E là giao điểm của AC và BD, F là giao điểm của AD và BC. Tính $\widehat{\mathrm{AEB}}$, $\widehat{\mathrm{AFB}}$

Cho AB và CD là hai đường kính vuông góc của đường tròn (O). trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES = EM.

Cho đường tròn (O), đường kính AB vuông góc với dây CD. Qua điểm M thuộc cung AD, kẻ tiếp tuyến với đường tròn, cắt CD ở I. Gọi E là giao điểm của BM và CD.

a) Chứng minh rằng IM = IE

b) Gọi F là giao điểm của AM và CD. Chứng minh rằng $\widehat{\mathrm{AFC}}=\widehat{\mathrm{ABM}}$

Một đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của các cung AB và AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh  là tam giác cân.

Cho $∆\mathrm{ABC}$ nhọn và AB < AC nội tiếp đường tròn tâm O. Gọi D, E, F lần lượt là điểm chính giữa của các cung nhỏ AB, BC, CA. Tiếp tuyến tại A của đường tròn cắt các đường thẳng BC và DF lần lượt tại M và N. Gọi P và Q lần lượt là giao điểm của đường thẳng BC với đường thẳng DF và AE.

a) Chứng minh rằng $\mathrm{AE}\perp \mathrm{DF}$

b) Chứng minh rằng MA = MQ, MN = MP

Từ một điểm M ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến MT và cát tuyến MAB đi qua tâm (A nằm giữa M và B). Giả sử số đo của cung nhỏ AT bằng ${60}^0$. Tính số đo của góc $\widehat{\mathrm{FMB}}$

Cho đường tròn (O; R) và hai đường kính AB, CD vuông góc với nhau. Trên tia AB lấy điểm M sao cho AM = $\mathrm{R}\sqrt{2}$. Vẽ dây CN đi qua điểm M. Từ N vẽ tiếp tuyến xy với đường tròn. Chứng minh rằng:

a) xy // AC

b) CN là tia phân giác của góc $\widehat{\mathrm{BCD}}$

Cho $∆\mathrm{ABC}$ cân tại A nội tiếp đường tròn (O). Đường phân giác của hai góc $\hat{\mathrm{B}}$ và $\hat{\mathrm{C}}$ cắt nhau ở E và cắt đường tròn ở F và D. Chứng minh rằng tứ giác EDAF là một hình thoi.

Qua điểm a nằm ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn. Chứng minh $\hat{\mathrm{A}}-\widehat{\mathrm{BSM}}=2\widehat{\mathrm{CMN}}$

Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho $\mathrm{sd}\stackrel{⏜}{\mathrm{AC}}=\mathrm{sd}\stackrel{⏜}{\mathrm{CD}}=\mathrm{sd}\stackrel{⏜}{\mathrm{DB}}={60}^0$. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

a) $\widehat{\mathrm{AEB}}=\widehat{\mathrm{BTC}}$

b) CD là tia phân giác của $\widehat{\mathrm{BCT}}$

Cho đường tròn (O) và hai dây cung bằng nhau AB, AC. Trên cung nhỏ AC lấy điểm M. Gọi I là giao điểm của AM và BC. Chứng minh rằng $\widehat{\mathrm{AIC}}=\widehat{\mathrm{ACM}}$