Tailieumoi.vn giới thiệu giải Chuyên đề Tin học lớp 11 Bài 5: Thực hành thiết kế thuật toán theo kĩ thuật đệ quy sách Kết nối tri thức hay, chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm Chuyên đề học tập Tin học 11. Mời các bạn đón xem:

Giải Chuyên đề Tin học 11 Bài 5: Thực hành thiết kế thuật toán theo kĩ thuật đệ quy

Khởi động trang 25 Chuyên đề Tin học 11: Hãy phân tích một số ưu nhược điểm của việc áp dụng kĩ thuật đệ quy trong lập trình

Lời giải:

* Ưu điểm:

- Code ngắn gọn, dễ đọc và dễ hiểu: Một số bài toán cần giải quyết có cấu trúc lặp đi lặp lại, nhưng sử dụng đệ quy giúp code được viết ngắn gọn hơn, dễ hiểu và dễ bảo trì.

- Dễ dàng để xử lý các bài toán phức tạp: Kỹ thuật đệ quy giúp chúng ta dễ dàng giải quyết các bài toán phức tạp hơn bằng cách chia nhỏ bài toán thành các bài toán con đơn giản hơn.

* Tuy nhiên, kỹ thuật đệ quy cũng có một số nhược điểm, như:

- Thời gian chạy chậm: Kỹ thuật đệ quy có thể làm cho chương trình chạy chậm hơn nếu sử dụng không chính xác.

- Khó hiểu: Trong một số trường hợp, kỹ thuật đệ quy có thể làm cho mã khó hiểu, đặc biệt là khi số lần đệ quy là lớn.

Luyện tập

Luyện tập 1 trang 27 Chuyên đề Tin học 11: Viết chương trình đệ quy giải quyết nhiệm vụ 2 nhưng với yêu cầu đầu ra của hàm là một dãy (list) các số 0 và 1

Lời giải:

Để chuyển từ số thập phân sang nhị phân bằng đệ quy, ta cần thực hiện các bước sau:

1. Chia số thập phân cho 2 và lấy phần nguyên và phần dư

2. Lưu phần dư vào danh sách

3. Lặp lại cho đến khi số thập phân bằng 0

Ví dụ, nếu ta gọi hàm decimal_to_binary(13), kết quả trả về sẽ là [1, 1, 0, 1], tương ứng với số nhị phân 1101.

Luyện tập 2 trang 27 Chuyên đề Tin học 11: Viết hàm decimal(s) chuyển đổi xâu nhị phân s sang số thập phân tương ứng. Ví dụ nếu đầu vào là "10" thì kết quả 2, nếu đầu vào "1011" thì kết quả là 11. Yêu cầu viết theo kĩ thuật đệ quy.

Lời giải:

Để chuyển đổi một xâu nhị phân sang số thập phân, ta có thể sử dụng thuật toán đệ quy như sau:

- Nếu xâu chỉ có một kí tự, trả về giá trị của kí tự đó (0 hoặc 1).

- Ngược lại, lấy kí tự đầu tiên của xâu và nhân với 2^(độ dài xâu - 1), sau đó cộng với giá trị của phần còn lại của xâu đã bỏ đi kí tự đầu tiên.

Ví dụ:

Vận dụng

Vận dụng 1 trang 27 Chuyên đề Tin học 11: Cho trước dãy số A = A[0], A[1], ...., A[n - 1]. Cặp phần tử (A[i], A[j]) được gọi là nghịch đảo nếu i < j nhưng A[i] > A[j]. Viết chương trình đếm số các cặp phần tử nghịch đảo của dãy A

a) Viết chương trình không đệ quy.

b) Viết chương trình theo kĩ thuật đệ quy

Lời giải:

a) Viết chương trình không đệ quy, sử dụng 2 vòng lặp

b) Viết chương trình theo kĩ thuật đệ quy, khá phức tạp

Vận dụng 2 trang 27 Chuyên đề Tin học 11: Thiết kế thuật toán cho bài toán tính giá trị của đa thức

(1)

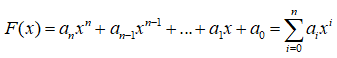
Ở đây, đầu vào là các giá trị $x,a_0,a_1,...,a_n$

Gọi A = $[a_0,a_1,...,a_n]$ là dãy các hệ số của đa thức (1).

Công thức (1) có thể viết lại với định nghĩa hàm F(A, x, n) như sau:

(2)

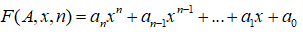
Lời giải:

Thuật toán:

- Nếu i = 0, ta trả về a[0]

- Ngược lại, ta tính giá trị của đa thức đến bậc i - 1, rồi nhân với x, cuối cùng cộng với a[i].

Viết chương tình và kiểm tra kết quả như sau:

Thu được kết quả:

Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 4: Tháp Hà Nội

Bài 5: Thực hành thiết kế thuật toán theo kĩ thuật đệ quy

Bài 6: Ý tưởng và kĩ thuật chia để trị

Bài 7: Thiết kế thuật toán theo kĩ thuật chia để trị

Bài 8: Thực hành thiết thuật toán tìm kiếm theo kĩ thuật chia để trị