Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các bài toán đặc sắc về tứ giác và đa giác, tài liệu bao gồm 50 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm có:

I. Lý thuyết

II. Bài tập

CÁC BÀI TOÁN VỀ TỨ GIÁC VÀ ĐA GIÁC ĐẶC SẮC

I. MỘT SỐ KIẾN THỨC VỀ TỨ GIÁC

1. Tứ giác

Định nghĩa:

Tứ giác ABCD là hình gồm đoạn thẳng AB, BC, CD, DA, trong bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tam giác.

Tính chất:

Tổng các góc của một tứ giác bằng 360^o.

Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác. Tổng các góc ngoài của một tứ giác bằng 360^o.

2. Hình thang

Định nghĩa

Hình thang là tứ giác có hai cạnh đối song song.

Hình thang vuông là hình thang có một góc vuông.

Tính chất

Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.

Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.

Hình thang cân

Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Tính chất: Trong hình thang cân hai cạnh bên bằng nhau và hai đường chéo bằng nhau.

Dấu hiệu nhận biết:

+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

+ Hình thang có hai đường chéo bằng nhau là hình thang cân.

Đường trung bình của tam giác

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Đường trung bình của hình thang

Đường trung bình của hình thang là đoạn thẳng nối trung điểm  hai cạnh bên của hình thang.

Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

3. Hình bình hành

Định nghĩa: Hình bình hành là tứ giác có các cặp cạnh đối song song.

Tính chất: Trong hình bình hành:

Các cạnh đối bằng nhau.

Các góc đối bằng nhau.

Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Dấu hiệu nhận biết:

Tứ giác có các cạnh đối song song là hình bình hành.

Tứ giác có các cạnh đối bằng nhau là hình bình hành

Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

4. Hình chữ nhât

Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.

Tính chất: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung ddierm của mỗi đường.

Dấu hiệu nhận biết:

Tứ giác có ba góc vuông là hình chữ nhật.

Hình thang cân có một góc vuông là hình chữ nhật.

Hình bình hành có một góc vuông là hình chữ nhật.

Hình bình hành có một góc vuông là hình chữ nhật.

Áp dụng vào tam giác:

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nữa cạnh huyền.

Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác vuông.

5. Hình thoi

Định nghĩa: Hình thoi là một tứ giác có bốn cạnh bằng nhau.

Tính chất: Trong hình thoi:

Hai đường chéo vuông góc với nhau

Hai đường chéo là các đường phân giác của các góc của hình thoi.

Dấu hiệu nhận biết:

Tứ giác có bốn cạnh bằng nhau là hình thoi.

Hình hình hành có hai cạnh kề bằng nhau là hình thoi.

Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

6. Hình vuông

Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.

Tính chất: Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.

Dấu hiệu nhận biết:

Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

Hình thoi có hai đường chéo bằng nhau là hình vuông.

Một tứ giác vừa là hình chữ nhật, vừa là hình thoi thì tứ giác đó là hình vuông.

7. Đa giác

Định nghĩa

Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Một số tính chất

Tồng các góc của đa giác n cạnh bằng \((n - 2){.180^o}\).

Mỗi góc của đa giác đều n cạnh bằng \(\frac{{\left( {n - 2} \right){{.180}^o}}}{n}\).

Số các đường chéo của đa giác n cạnh bằng \(\frac{{n(n - 3)}}{2}\).

II. CÁC VÍ DỤ MINH HOẠ

Ví dụ 1. Cho tứ giác ABCD. Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau khi và chỉ khi \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\)

Phân tích tìm lời giải

Dễ thấy nếu tứ giác ABCD có hai đường chéo vuông góc thì \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\), ngược lại nếu có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\), khi đó để chứng minh AC và BD vuông góc với nhau ta có các hướng sau:

+ Hướng 1: Gọi M là giao điểm của AC và BD. Từ đỉnh B hạ đường vuông góc với AC tại O. Ta cần chứng minh được M và O trùng nhau. Muốn vậy lấy N trên tia đối của tia OB sao cho ON = MD và ta cần phải chứng minh được hai điểm M và O trùng nhau. Chú ý rằng khi AB = BC thì ta suy ra được CD = DA  nên hiển nhiên M và O trung nhau. Như vậy ta cần xét cho trường hợp \(AB \ne BC\). Theo định lí Pitago ta có

\(A{B^2} + C{D^2} = A{M^2} + 2AM.OM + O{M^2} + O{B^2} + C{M^2} + M{D^2}\)

\(B{C^2} + A{D^2} = O{B^2} + M{C^2} - 2MC.OM + O{M^2} + O{B^2} + M{A^2} + M{D^2}\)

Mà ta lại có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\) nên từ đó ta suy ra được \(MO\left( {AM + MC} \right) = 0 \Leftrightarrow MO = 0\)

+ Hướng 2: Dựng BK và DH cùng vuông góc với AC. Ta cần chứng minh cho hai điểm K và H trùng nhau. Áp dụng định lí Patago ta được

\(A{B^2} + C{D^2} = A{K^2} + B{K^2} + C{H^2} + D{H^2}\); \(B{C^2} + A{D^2} = C{K^2} + B{K^2} + A{H^2} + D{H^2}\)

Mà ta có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\) nên ta được KH = 0.

Lời giải

+ Điều kiện cần: Xét tứ giác ABCD có hai đường chéo AC và BD vuông góc tại O

Khi đó áp dụng định lí Pitago ta được

\(A{B^2} + C{D^2} = O{A^2} + O{B^2} + O{C^2} + O{D^2}\); \(A{D^2} + B{C^2} = O{A^2} + O{B^2} + O{C^2} + O{D^2}\)

Từ đó ta được \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\).

+ Điều kiện đủ: Xét tứ giác ABCD có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\).

Cách 1: Ta xét các trường hợp sau

Nếu AB = BC thì từ \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\)ta được CD = DA

Từ đó suy ra B, D thuộc đường trung trực của đoạn thẳng AC, do đó \(AC \bot BD\).

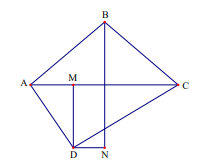
Nếu \(AB \ne BC\). Khi đó vẽ BO vuông góc với AC tại O, vẽ DM vuông góc với BO tại N. Khi đó tứ giác DMNO là hình chữ nhật.

Không mất tính tổng quát ta giả sử M nằm giữa O và A.

Khi đó áp dụng định lí Pitago ta được

\(\begin{array}{l}A{B^2} + C{D^2} = O{A^2} + O{B^2} + C{M^2} + M{D^2}\\ = {\left( {MA + MO} \right)^2} + O{B^2} + C{M^2} + M{D^2}\end{array}\)

\( = A{M^2} + 2AM.OM + O{M^2} + O{B^2} + C{M^2} + M{D^2}\)

\(\begin{array}{l}B{C^2} + A{D^2} = O{B^2} + O{C^2} + M{A^2} + M{D^2}\\ = O{B^2} + {\left( {MC - OM} \right)^2} + M{A^2} + M{D^2}\end{array}\)

\( = O{B^2} + M{C^2} - 2MC.OM + O{M^2} + M{A^2} + M{D^2}\)

Mà ta lại có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\) nên ta được

\(2MA.OM =  - 2MC.OM \Leftrightarrow MO\left( {AM + MC} \right) = 0 \Leftrightarrow MO = 0\)

Từ đó dẫn đến hai điểm O và M trùng nhau hay ta được \(AC \bot BD\).

Cách 2: Vẽ DH vuông góc với AC tại H, BK vuông góc với AC tại K

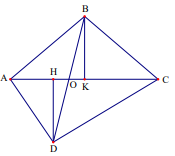
Nếu hai điểm K và H trùng nhau thì ta được \(AC \bot BD\)

Nếu hai điểm K và H không trùng nhau, khi đó gọi O là giao điểm của AC và BD. Không mất tính tổng quát ta giả sử A, H, O, K, C nằm trên AC theo thứ tự đó.

Áp dụng định lí Pitago ta được

\(A{B^2} + C{D^2} = A{K^2} + B{K^2} + C{H^2} + D{H^2}\)

\(B{C^2} + A{D^2} = C{K^2} + B{K^2} + A{H^2} + D{H^2}\)

Mà ta có \(A{B^2} + C{D^2} = A{D^2} + B{C^2}\) nên ta được

\(A{H^2} + C{H^2} = C{K^2} + A{H^2} \Leftrightarrow A{H^2} - C{H^2} + C{K^2} - A{K^2} = 0\)

\( \Leftrightarrow \left( {AH + CH} \right)\left( {AH - CH} \right) + \left( {AK + CK} \right)\left( {CK - AK} \right) = 0\)

\( \Leftrightarrow AC\left( {AH - CH + CK - AK} \right) = 2AC.KH \Leftrightarrow KH = 0\)

Điều này vô lí vì K không trùng nhau. Vậy hai điểm K và H trùng nhau hay ta được \(AC \bot BD.\)

Ví dụ 2. Cho tứ giác ABCD có hai đường chéo bằng nhau. Lấy các điểm E, F,G, H theo thứ tự chia trong các cạnh AB, BC, CD, DA theo tỉ số 1:2. Chứng minh rằng EG = FH và \(EG \bot FH.\)

Phân tích tìm lời giải

Từ giả thiết của bài toán ta suy ra được \(\frac{{BE}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{3}\) nên EM//AC. Tương tự ta cũng được NF//BD. Từ đó ta được \(EM = \frac{2}{3}AC\); \(NF = \frac{2}{3}BD\), chú ý đến AC = BD suy ra được ME = NF. Từ các đường thẳng song song ta thấy được \(MG = NH = \frac{1}{3}AC\) và