Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề các bài toán quỹ tích - tập hợp điểm, tài liệu bao gồm 31 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tài liệu gồm có:

I. Lý thuyết

II. Bài tập

BÀI TOÁN VỀ QUỸ TÍCH – TẬP HỢP ĐIỂM

I. MỘT SỐ KIẾN THỨC CẦN NHỚ

1. Định nghĩa tập hợp điểm (quỹ tích)

Một hình H được gọi là tập hợp điểm của những điểm M thoả mãn tính chất T khi nó chứa và chỉ chứa tính chất T

2. Phương pháp chủ yếu giải bài toán hợp điểm

Để tìm tập hợp các điểm M thoả mãn tính chất T ta làm như sau:

Bước 1: Tìm cách giải.

- Xác định các yếu tố cố định và không đổi

- Xác định các điều kiện của điểm M

- Dự đoán tập hợp điểm

Bước 2: Trình bày lời giải

Phần thuận: Chứng minh điểm M có tính chất T thuộc hình H

Giới hạn: Căn cứ vào các vị trí đặc biệt của điểm M, chứng tỏ điểm M chỉ thuộc vào hình H, hoặc một phần B của hình H (nếu được)

Phần đảo: Chứng minh mọi điểm thuộc H (quỹ tích đã được giới hạn) có tính chất T. Thường làm như sau:

+ Lấy điểm M thuộc hình H (quỹ tích đã được giới hạn), giả sử tính chất T gồm n điều kiện.

+ Dựng một hình để chứng minh M có tính chất T sao cho M thoả mãn n - 1 điều kiện trong tính chất T và chứng minh M có thoả mãn điều kiện còn lại.

Kết luận: Tập hợp điểm M là hình H. Nêu rõ hình dạng và cách xác định hình H.

Chú ý:

Cc

- Việc tìm ra mối liên hệ giữa các yếu tố cố định, không đổi với yếu tố chuyển động là khâu chủ yếu giúp ta giải quyết bài toán tập hợp điểm.

- Nếu bài toán chỉ hỏi “ Điểm M chuyển động trên đường nào?” thì ta chỉ trình bày phần thuận, phần giới hạn và phần kết luận mà không cần không chứng minh phần đảo.

- Giải bài toán tập hợp điểm thường là tìm cách đưa về tập hợp điểm cơ bản đã học

- Để khỏi vẽ hình lại khi chứng minh phần đảo tên các điểm trong phần đảo nên giữ nguyên như phần thuận.

3. Một số tập hợp điểm cơ bản

a) Tập hợp điểm là đường trung trực hoặc một phần đường trung trực

Định lí: Tập hợp các điểm M cách đều hai điểm phân biệt A, B cố định là đường trung trực d của đoạn thẳng AB

b) Tập hợp điểm là tia phân giác

Định lí: Tập hợp các điểm nằm trong góc xOy (khác góc bẹt) và cách đều hai cạnh của góc là tia phân giác của góc đó.

Hệ quả: Tập hợp các điểm M cách đều hai đường thẳng cắt nhau $xO{x}^{\text{'}}$và $yO{y}^{\text{'}}$ là bốn tia phân giác của bốn góc tạo thành, bốn tia này tạo thành hai đường thẳng vuông góc với nhau tại giao điểm O của hai đường thẳng đó.

c) Tập hợp điểm là đường thẳng song song

Định lý 1: Tập hợp các điểm M cách đường thẳng h cho trước một khoảng bằng a không đổi là hai đường thẳng song song với đường thẳng đã cho và cách đường thẳng đó bằng a.

Định lý 2: Tập hợp các điểm cách đều hai đường thẳng song song cho trước là một đường thẳng song song và nằm cách đều hai đường thẳng đã cho.

d) Tập hợp điểm là đường tròn, một phần của đường tròn, cung chứa góc.

+ Tập hợp các điểm M cách điểm O cho trước một khoảng không đổi r là đường tròn tâm O bán kính r.

+ Tập hợp các điểm nhìn đoạn thẳng cố định AB dưới góc 90^o là đường tròn đường kính AB.

+ Tập hợp các điểm M tạo thành với hai mút của đoạn thẳng AB cho trước một góc AMB có số đo không đổi là \(\alpha \left( {{0^o} < \alpha  < {{180}^o}} \right)\) là hai cung tròn đối xứng nhau qua AB.

II. CÁC VÍ DỤ MINH HOẠ

Ví dụ 1. Cho hình vuông ABCD. Tìm tập hợp điểm M trong mặt phẳng sao cho MA + MB = MC + MD

Lời giải

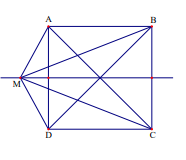
Phần thuận: Dựng đường thẳng d đi qua tâm O của hình vuông và d song song với AB, DC. Khi đó d là đường trung trực của AD và của BC. Ta thấy với mọi điểm M không thuộc đường thẳng d thì ta có \(MA + MB \ne MC + MD\)

+ \(MA + MB > MC + MD\) khi điểm M nằm khác phía với điểm A so với đường thẳng d;

+ \(MA + MB < MC + MD\) khi điểm M nằm cùng phía với điểm A so với đường thẳng d.

Vậy điểm \(MA + MB = MC + MD\) thì M thuộc đường trung trực d của AD và BC

Giới hạn: Mọi điểm M thuộc d đều có MA = MD và MB = MC nên \(MA + MB = MC + MD\). Vậy M thuộc đường thẳng d.

Phần đảo: Lấy M bất kỳ thuộc đường thẳng d thì ta có MA = MD và MB = MC.

Khi đó ta có MA + MB = MC + MD

Kết luận: Tập hợp điểm M cần tìm là đường trung trực của AD và Bc.

Ví dụ 2. Cho một góc vuông xOy, trên tia Ox lấy điểm A cố định, B là điểm chuyển động tia Oy. Tìm tập hợp các điểm C sao cho \(\Delta \)ABC vuông cân tại C.

Lời giải

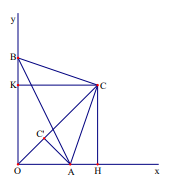
Phần thuận: Vẽ CH vuông góc với Ox (H thuộc Ox) và CK vuông góc với Oy (K thuộc Oy). Xét hai tam giác vuông CAH và CBK có CA = CB và CAH = CBK do đó \(\Delta CAH = \Delta CBK\)

Từ đó ta được CH = CK. Mà góc xOy cố định nên do đó C thuộc tia phân giác Oz của góc vuông xOy.

Giới hạn: Khi B trùng với O thì C trùng với C^’, điểm C^’ thuộc tia phân giác Oz và tam giác C^’OA vuông cân tại C^’. Khi B chạy xa O vô tận trên tia Oy thì C chạy xa O vô tận trên tia Oz. Vậy C chuyển động trên tia C^’z của tia phân giác Oz của góc vuông xOy.

Phần đảo: Lấy điểm C bất kỳ thuộc tia C^’z. Vẽ đường thẳng vuông góc CA tại C cắt tia Oy tại B. Vẽ CH vuông góc với Ox (H thuộc Ox) và CK vuông góc với Oy (K thuộc Oy). Ta có CH = CK và KHC = 90^o.

Xét hai tam giác vuông CAH và CBK có CH = CK và CAH = CBK nên \(\Delta CAH = \Delta CBK\)

Từ đó ta được CA = CB do đó tam giác ABC vuông cân tại C.

Kết luận: Tập hợp các điểm C là tia C^’z của tia phân giác Oz của góc xOy.

Ví dụ 3. Cho tam giác ABC và điểm M di chuyển trên cạnh BC. Tìm quỹ tích các trung điểm I của đoạn thẳng AM.

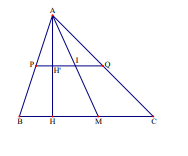
Phần thuận: Kẻ đường cao AH của tam giác ABC với H thuộc BC. Từ I kẻ IK vuông góc với BC (K thuộc BC). Từ đó IK//AH.

Xét tam giác MAH có IM = IA và IK//AH nên IK là đường trung bình của tam giác AMH. Do đó ta được \(IK = \frac{1}{2}AH\)

Mà tam giác ABC cố định nên AH cố định, suy ra \(IK = \frac{1}{2}AH\) không đổi.

Vậy điểm I luôn cách BC một đoạn \(IK = \frac{1}{2}AH\) không đổi nên I nằm trên đường thẳng song song với BC và cách BC một khoảng là \(\frac{1}{2}AH\).

Giới hạn: Vì A, I cùng nằm trong mặt phẳng bờ là đường thẳng BC nên I nằm trên đường thẳng xy//BC và cách BC một khoảng \(\frac{1}{2}AH\) cùng phía đối với đường thẳng BC.

+ Khi \(M \equiv B\) thì \(I \equiv P\) với P là trung điểm AB.

+ Khi \(M \equiv C\) thì \(I \equiv Q\) với Q là trung điểm AC.

Khi M chạy trên cạnh BC thì điểm I chạy trên đoạn thẳng PQ (thuộc đường thẳng xy) và PQ là đường trung bình của tam giác ABC (\(P \in AB\), \(Q \in AC\))

Phần đảo: Lấy điểm I thuộc đường trung bình PQ của tam giác ABC, tia AI cắt BC ở M. Vì \(I \in PQ\) nên tia AI nằm giữa 2 tia AB, AC và do vậy M thuộc đoạn.

Từ I kẻ IK vuông góc với BC. Vì I thuộc PQ nên ta được \(IK = \frac{1}{2}AH\)

Mặt khác ta có IK vuông góc với BC và AH vuông góc với BC nên ta được IK//AH.

Gọi $H^{\text{'}}$ là giao điểm của AH và PQ.

Xét hai tam giác $AI{H}^{\text{'}}$ và IMK có $IK=A{H}^{\text{'}}=\frac{1}{2}AH$, $IK=A{H}^{\text{'}}=\frac{1}{2}AH$ và $MIK=IA{H}^{\text{'}}$

Do đó ta được $\Delta AI{H}^{\text{'}}=\Delta IMK$ nên suy ra IA = IM hay I là trung điểm của AM.

Kết luận: Vậy quỹ tích trung điểm I của đoạn AM là đường trung bình PQ của tam giác ABC với P thuộc cạnh AB, Q thuộc cạnh AC.

Ví dụ 4: Cho góc vuông xOy cố định, điểm A cố định trên Oy, điểm B di động trên Ox. Tìm tập hợp các trung điểm M của AB.

Lời giải

Phần thuận: Ta có \(OM = \frac{{AB}}{2}\) (trung tuyến ứng với cạnh huyền của tam giác vuông AOB).

Mà ta có \(MA = \frac{{AB}}{2}\), suy ra MA = OM không đổi.