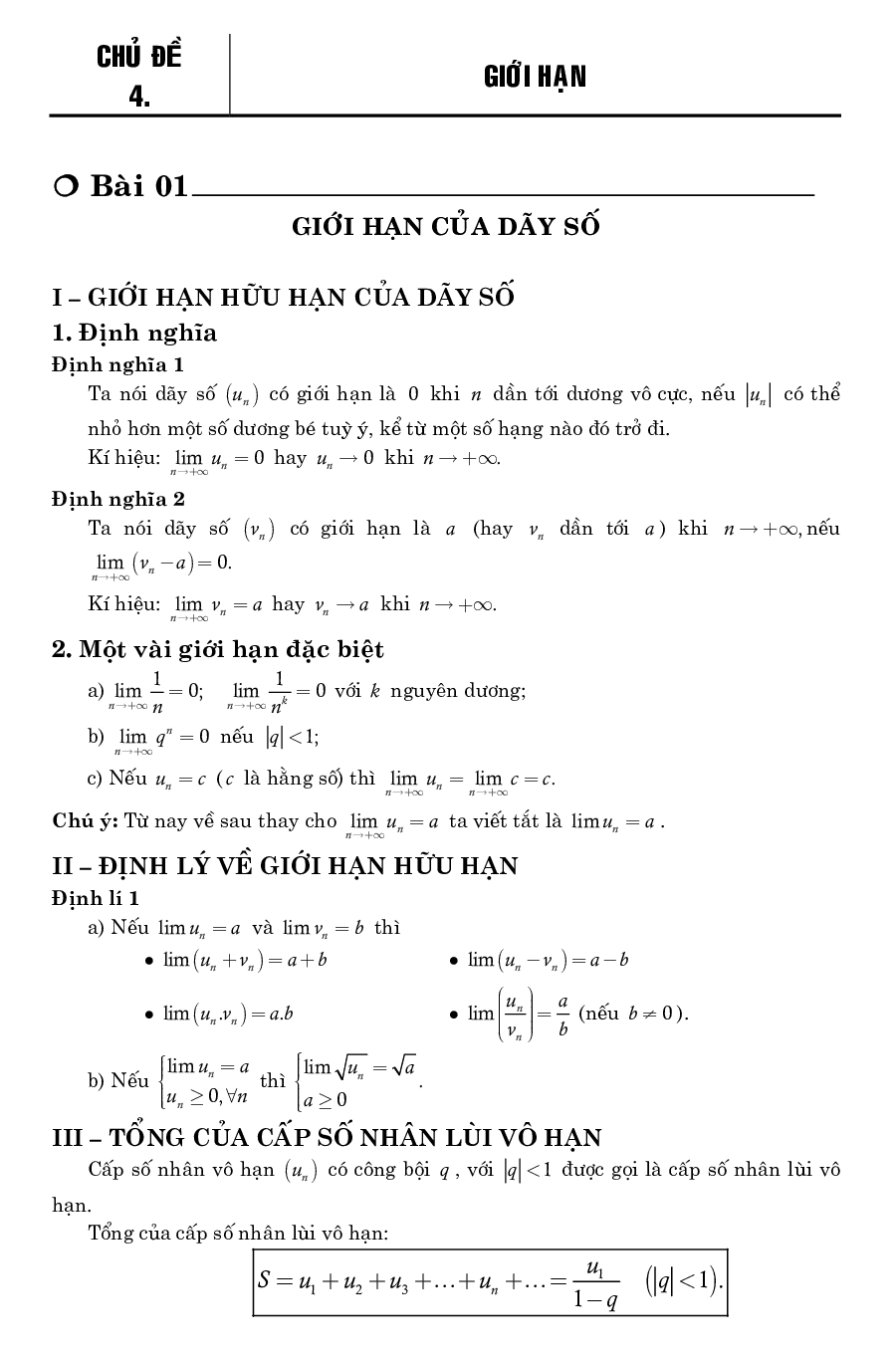Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập trắc nghiệm về giới hạn có lời giải chi tiết, tài liệu bao gồm 58 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu gồm những phần chính:
I. Lý thuyết.
II. Câu hỏi trắc nghiệm có đáp án.
CHỦ ĐỂ 4. GIỚI HẠN
Bài 01:
GIỚI HẠN CỦA DÃY SỐ
I – GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
1. Định nghĩa
Định nghĩa 1
Ta nói dã số \(({u_n})\)có giới hạn là 0 khi n dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Kí hiệu: \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\) khi \(n \to + \infty \).
Định nghĩa 2
Ta nói dã số (vn) có giới hạn là a (hay vn dần tới a) khi \(n \to + \infty \), nếu \(\mathop {\lim }\limits_{x \to + \infty } ({v_n} - a) = 0\) .
Kí hiệu: \(\mathop {\lim }\limits_{x \to + \infty } {v_n} = a\) hay \(\)\({v_n} \to a\) khi \(n \to + \infty \).
2. Một vài giới hạn đặc biệt
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{n} = 0;\) \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{n^k}}} = 0\) với k nguyên dương;
b) \(\mathop {\lim }\limits_{x \to + \infty } {q^n} = 0\) nếu \(\)\(\left| q \right| < 1\);
c) Nếu \({u_n} = c\) (c là hằng số) thì \(\)\(\mathop {\lim }\limits_{x \to + \infty } {u_n} = \mathop {\lim }\limits_{x \to + \infty } c = c.\)
Chú ý: Từ nay về sau thay cho \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a\) ta viết tắt là \(\)\(\lim {u_n} = a\)
II- ĐỊNH LÝ VỀ GIỚI HẠN HỮU HẠN
Định lí 1
a) Nếu \(\lim {u_n} = a\) và \(\lim {v_n} = b\) thì
lim(un+vn)=a+b
lim(un-vn)=a-b
lim(un.vn)=a.b
\(\lim \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = \frac{a}{b}\) (nếu \(\)\(b \ne 0\))
b) Nếu \(\left\{ \begin{array}{l}\lim {u_n} = a\\{u_n} \ge 0,\forall n\end{array} \right.\) thì \(\left\{ \begin{array}{l}\lim \sqrt {{u_n}} = \sqrt a \\a \ge 0\end{array} \right.\)
III- TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
Cáp số nhân vô hạn (un) có công bội q, với \(\)\(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn:
IV- GIỚI HẠN VÔ CỰC
1. Định nghĩa
Ta nói dã số (un) có giới hạn là \(\)\( + \infty \) khi \(n \to + \infty \), nếu un có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Kí hiệu: \(\lim {u_n} = + \infty \) hay \(\)\({u_n} \to + \infty \), nếu \(\lim ( - {u_n}) = + \infty \).
Dãy số (un) có giới hạn là \( - \infty \) khi \(n \to + \infty \), nếu \(\lim \left( { - {u_n} = + \infty } \right)\)
Kí hiệu: \(\lim {u_n} = - \infty \) hay \({u_n} \to - \infty \) khi \(n \to + \infty \)
Nhận xét: \({u_n} = + \infty \Leftrightarrow \lim \left( { - {u_n}} \right) = - \infty \).
2. Một vài giới hạn đặc biệt
Ta thừa nhận các kết quả sau
a) \(\lim {n^k} = + \infty \) với k nguyên dương;
b) \(\lim {q^n} = + \infty \) nếu q > 1.
3. Định lí 2
a) Nếu lim un = a và \(\lim {v_n} = \pm \infty \) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = 0.\)
b) Nếu lim un = a > 0, lim vn = 0 và \({v_n} > 0,\forall n > 0\) thì \(\lim \frac{{{u_n}}}{{{v_n}}} = + \infty .\)
c) Nếu \(\lim {u_n} = + \infty \) và lim vn = a > 0 thì \({u_n},{v_n} = + \infty .\)
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. DÃY SỐ DẠNG PHÂN THỨC
Câu 1. Kết quả của giới hạn \(\lim \left( {\frac{{\sin 5n}}{{3n}} - 2} \right)\) bằng:
A. -2.
B. 3.
C. 0.
D. \(\frac{5}{3}\).
Lời giải. Ta có \(0 \le \left| {\frac{{\sin 5n}}{{3n}}} \right| \le \frac{1}{n}\), mà \(\lim \frac{1}{n} = 0\) nên \(\lim \frac{{\sin 5n}}{{3n}} = 0\) do đó \(\lim \left( {\frac{{\sin 5n}}{{3n}} - 2} \right) = - 2\). Chọn A.
Nhận xét: Có thể dùng MTCT để tính (có thể chính xác hoặc gần đúng) giới hạn như sau (các bài tập sau có thể làm tương tự):
Nhập \(\frac{{\sin \left( {5X} \right)}}{{3X}} - 2.\)
Bấm CALC và nhập 9999999999 (một số dòng MTCT kho bấm nhiều số <<9>> thì nó báo lỗi, khi đó ta cần bấm ít số <<9>> hơn.
Bấm <<=>> ta được kết quả (có thể gần đúng), sau đó chọn đáp án có giá trị gần đúng với kết quả hiện trên MTCT.
Câu 2. Có bao nhiêu số tự nhiên chẵn k để \[\lim \frac{{n - 2\sqrt {{n^k}} \cos \frac{1}{n}}}{{2n}} = \frac{1}{2}.\]
A. 0.
B. 1.
C. 4.
D. Vô số.
Lời giải. Ta có \(\frac{{n - 2\sqrt n \sin 2n}}{{2n}} = \frac{1}{2} - \frac{{\sqrt n \sin 2n}}{n}.\)
Điều kiện bài toán trở thành \(\lim \frac{{\sqrt {{n^k}} \cos \frac{1}{n}}}{n} = 0.\)
Ta có \(\lim \cos \frac{1}{n} = \cos 0 = 1\) nên bài toán trờ thành tìm k sao cho \(\lim \frac{{\sqrt {{n^k}} }}{n} = \lim {n^{\frac{k}{2} - 1}} = 0 \Leftrightarrow \frac{k}{2} - 1 < 0 \Leftrightarrow k < {2_{\overrightarrow {k \in {\mathbb{N}^*},k = 3l} }}\) không tồn tại k (do k nguyên dương và chẵn). Chọn A.
Câu 3. Kết quả của giới hạn \(\lim \frac{{3\sin n + 4\cos n}}{{n + 1}}\) bằng:
A. 1.
B. 0.
C. 2.
D. 3.
Lời giải. Ta có \(0 \le \left| {\frac{{3\sin n + 4\cos n}}{{n + 1}}} \right| \le \frac{7}{{n + 1}} \le \frac{7}{n} \to 0 \to \lim \frac{{3\sin n + 4\cos n}}{{n + 1}} = 0\). Chọn B.
Câu 4. Kết quả của giới hạn \(\lim \left( {5 - \frac{{n\cos 2n}}{{{n^2} + 1}}} \right)\) bằng:
A. 4.
B. \(\frac{1}{4}\).
C. 5.
D. -4.
Lời giải. Ta có
\(\begin{array}{l}0 \le \left| {\frac{{n\cos 2n}}{{{n^2} + 1}}} \right| \le \frac{n}{{{n^2} + 1}} \le \frac{1}{n} \to 0\\ \to \lim \frac{{n\cos 2n}}{{{n^2} + 1}} = 0 \to \lim \left( {5 - \frac{{n\cos 2n}}{{{n^2} + 1}}} \right) = 5\end{array}\)
Chọn C.
Câu 5. Kết quả của giới hạn \(\lim \left( {{n^2}\sin \frac{{n\pi }}{5} - 2{n^3}} \right)\) là:
A. \( - \infty \).
B. -2.
C. 0.
D.\( + \infty \).
Lời giải. Ta có \(\lim \left( {{n^2}\sin \frac{{n\pi }}{5} - 2{n^3}} \right) = \lim {n^3}\left( {\frac{1}{n}.\frac{{\sin n\pi }}{5} - 2} \right).\) Vì
\(\)\[\begin{array}{l}\left\{ \begin{array}{l}\lim {n^3} = + \infty \\0 \le \left| {\frac{1}{n}.\frac{{\sin n\pi }}{5}} \right| \le \frac{1}{n} \to 0\overrightarrow {\,\,\,\,\,\,\,\,\,} \end{array} \right.\left\{ \begin{array}{l}\lim {n^3} = + \infty \\\lim \left( {\frac{1}{n}.\frac{{\sin n\pi }}{5} - 2} \right) = - 2 < 0\end{array} \right.\\\overrightarrow {\,\,\,\,\,\,\,\,\,} \lim {n^3}\left( {\frac{1}{n}.\frac{{\sin n\pi }}{5} - 2} \right) = - \infty .\end{array}\]
Chọn A.
Câu 6. Giá trị của giới hạn \(\lim \left( {4 + \frac{{{{\left( { - 1} \right)}^n}}}{{n + 1}}} \right)\) bằng:
A. 1.
B. 3.
C. 4.
D. 2.
Lời giải: Ta có
Chọn C.
Câu 7. Cho hai dãy số (un) và (vn) có \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{n^2} + 1}}\) và \({v_n} = \frac{1}{{{n^2} + 2}}\). Khi đó \(\lim \left( {{u_n} + {v_n}} \right)\) có giá trị bằng:
A. 3.
B. 0.
C. 2.
D. 1.
Lời giải. Ta có
\(\)
Chọn B.
Chú ý: Cho P(n), Q(n) lần lượt là các đa thức bậc m, k theo biến n:
\(P\left( x \right) = {a_m}{n^m} + {a_{m - 1}}{n^{m - 1}} + ... + {a_1}n + {a_0}\left( {{a_m} \ne 0} \right)\)
\(Q\left( n \right) = {b_k}{n^k} + {b_{k - 1}}{n^{k - 1}} + ... + {b_1}n + {b_0}\left( {{b_k} \ne 0} \right)\)
Khi đó \(\lim \frac{{P\left( n \right)}}{{Q\left( n \right)}} = \lim \frac{{{a_m}{n^m}}}{{{b_k}{n^k}}}\), viết tắt \(\frac{{p\left( n \right)}}{{Q\left( n \right)}} \sim \frac{{{a_m}{n^m}}}{{{b_k}{n^k}}}\), ta có các trường hợp sau:
Nếu <<bậc tử>> < <<bậc mẫu (m < k) thì \(\lim \frac{{P\left( n \right)}}{{Q\left( n \right)}} = 0.\)
Nếu <<bậc tử>> = <<bậc mẫu (m = k) thì \(\lim \frac{{P\left( n \right)}}{{Q\left( n \right)}} = \frac{{{a_m}}}{{{b_k}}}.\)
Nếu <<bậc tử>> > <<bậc mẫu (m > k) thì \(\lim \frac{{P\left( n \right)}}{{Q\left( n \right)}} = \left\{ \begin{array}{l} + \infty \,\,khi\,{a_m}{b_k} > 0\\ - \infty \,\,khi\,{a_m}{n_k} < 0\end{array} \right.\).
Để ý rằng nếu P(n), Q(n) có chứa <<căn>> thì ta vẫn tính được bậc của nó. Cụ thể \(\sqrt[m]{{{n^k}}}\)thì có bậc là \(\frac{k}{n}\). Ví dụ \(\sqrt n \) có bậc là \(\frac{1}{2},\,\sqrt[3]{{{n^4}}}\) có bậc là \(\frac{4}{3}\), …
Trong các bài sau ta có thể dùng dấu hiệu trên để chỉ ra kết quả một cách nhanh chóng!
Câu 8. Giá trị của giới hạn \(\lim \frac{{ - 3}}{{4{n^2} - 2n + 1}}\) là:
A. \( - \frac{3}{4}\).
B. \( - \infty .\)
C. 0.
D. -1.
Lời giải. Ta có \(\lim \frac{{ - 3}}{{4{n^2} - 2n + 1}} = \lim \frac{{\frac{{ - 3}}{{{n^2}}}}}{{4 - \frac{2}{n} + \frac{1}{{{n^2}}}}} = \frac{0}{4} = 0\). Chọn C.
Giải nhanh: Dạng <<bậc tử>> < <<bậc mẫu>> nên kết quả bằng 0.
Câu 9. Giá trị của giới hạn \(\lim \frac{{n + 2{n^2}}}{{{n^3} + 3n - 1}}\) bằng:
A. 2.
B. 1.
C. \(\frac{2}{3}\).
D. 0.
Lời giải. Ta có \(\lim \frac{{n + 2{n^2}}}{{{n^3} + 3n - 1}} = \lim \frac{{\frac{1}{{{n^2}}} + \frac{2}{n}}}{{1 + \frac{3}{{{n^2}}} - \frac{1}{{{n^3}}}}} = \frac{0}{1} = 0\). Chọn D.
Giải nhanh: Dạng <<bậc tử>> < <<bậc mẫu>> nên kết quả bằng 0.
Câu 10. Giá trị của giới hạn \(\lim \frac{{3{n^3} - 2n + 1}}{{4{n^4} + 2n + 1}}\) là:
A. \( + \infty \).
B. 0.
C. \(\frac{2}{7}\).
D. \(\frac{3}{4}\).
Lời giải. Ta có \(\lim \frac{{3{n^3} - 2n + 1}}{{4{n^4} + 2n + 1}} = \lim \frac{{\frac{3}{n} - \frac{2}{{{n^2}}} + \frac{1}{{{n^4}}}}}{{4 + \frac{2}{{{n^3}}} + \frac{1}{{{n^4}}}}} = \frac{0}{4} = 0\). Chọn B.
Giải nhanh: Dạng <<bậc tử>> < <<bậc mẫu>> nên kết quả bằng 0.
Câu 11. Giá trị của giới hạn \(\lim \frac{{n\sqrt n + 1}}{{{n^2} + 2}}\) bằng:
A. \(\frac{3}{2}\).
B. 2.
C. 1.
D. 0.
Lời giải. Ta có \(\lim \frac{{n\sqrt n + 1}}{{{n^2} + 2}} = \lim \frac{{\frac{1}{{\sqrt n }} + \frac{1}{{{n^2}}}}}{{1 + \frac{2}{{{n^2}}}}} = \frac{0}{1} = 0.\) Chọn D.
Giải nhanh: \(\lim \frac{{n\sqrt n + 1}}{{{n^2} + 2}} \sim \frac{{n\sqrt n }}{{{n^2}}} = \frac{1}{{\sqrt n }} \to 0.\)
Câu 12. Cho hai dãy số (un) và (vn) có \({u_n} = \frac{1}{{n + 1}}\) và \({v_n} = \frac{2}{{n + 2}}\). Khi đó \(\lim \frac{{{v_n}}}{{{u_n}}}\) có giá trị bằng:
A. 1.
B. 2.
C. 0.
D. 3.
Lời giải. Ta có \(\lim \frac{{{v_n}}}{{{u_n}}} = \lim \frac{{n + 1}}{{n + 2}} = \lim \frac{{1 + \frac{1}{n}}}{{1 + \frac{2}{n}}} = \frac{1}{1} = 1.\) Chọn A.
Giải nhanh: \(\frac{{n + 1}}{{n + 2}} \sim \frac{n}{n} = 1.\)
Câu 13. Cho dãy số (un) với \({u_n} = \frac{{an + 4}}{{5n + 3}}\) trong đó a là tham số thực. Để dãy số (un) có giới hạn bằng 2, giá trị của a là: