Đề thi HSG Toán 12 cấp quốc gia năm 2023

Đề thi HSG Toán 12 cấp quốc gia năm 2023 - 2024 bộ GD&ĐT

Trịnh Thị Thu Hiền Ngày: 27-06-2024 Lớp 12

Tải xuống 17 298 2

Tailieumoi.vn xin giới thiệu đề thi học sinh giỏi Toán lớp 12 quốc gia năm 2023 - 2024 bộ GD&ĐT có lời giải chi tiết. Hi vọng với bộ tài liệu này các em ôn luyện, củng cố kiến thức, rèn luyện kĩ năng làm bài thật tốt để bước bài kì thi HSG sắp tới.

Đề thi HSG Toán 12 quốc gia năm 2023 - 2024 bộ GD&ĐT

Một số câu hỏi có trong đề thi:

Câu 1 (5,0 điểm)

Với mỗi số thực x, ta gọi [x] là số nguyên lớn nhất không vượt quá x.

Cho dãy số ${\{a_{n}\}}^{\infty}_{n = 1}$ xác định bởi $a_{n} = \frac{1}{4^{[- \log_{4} n]}}, \forall n \geq 1 .$ Đặt $b_{n} = \frac{1}{n^{2}} (\sum_{k = 1}^{n} a_{k} - \frac{1}{a_{1} + a_{2}}), \forall n \geq 1 .$

a) Tìm một đa thức P(x) với hệ số thực sao cho $b_{n} = P (\frac{a_{n}}{n}), \forall n \geq 1 .$

b) Chứng minh rằng tồn tại một dãy số nguyên dương ${\{n_{k}\}}^{\infty}_{k = 1}$ tăng thực sự sao cho

$\lim_{k \to \infty} b_{n_{k}} = \frac{2024}{2025} .$

Câu 2 (5,0 điểm)

Tìm tất cả các đa thức P(x), Q(x) với hệ số thực sao cho với mỗi số thực a thì P(a) là nghiệm của phương trình $x^{2023} + Q (a) . x^{2} + (a^{2024} + a) x + a^{3} + 2025 a = 0 .$

Câu 3 (5,0 điểm)

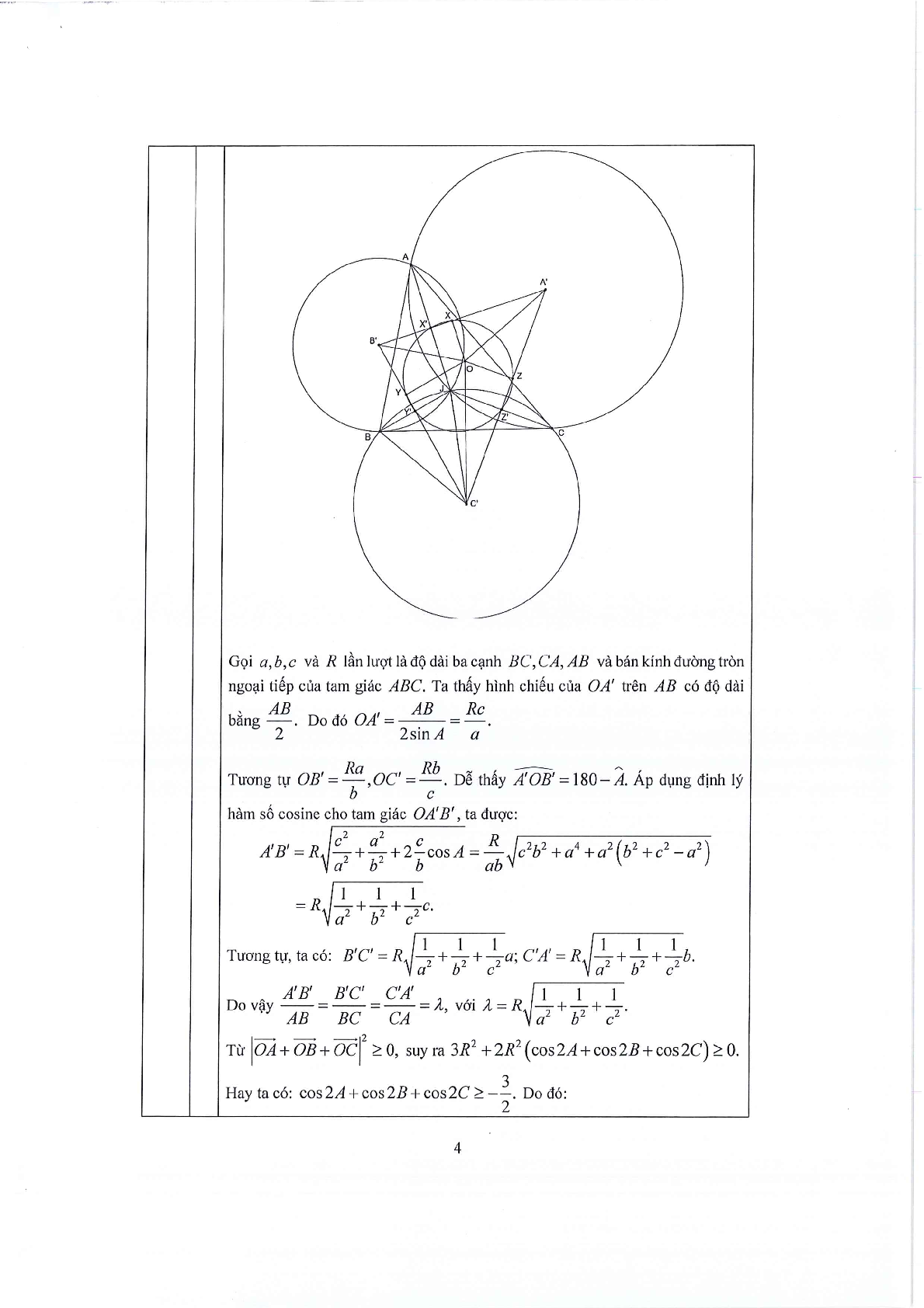
Cho ABC là tam giác nhọn với tâm đường tròn ngoại tiếp O. Gọi A' là tâm của đường tròn đi qua C và tiếp xúc AB tại A, gọi B' là tâm của đường tròn đi qua A và tiếp xúc BC tại B, gọi C' là tâm đường tròn đi qua B và tiếp xúc CA tại C.

a) Chứng minh rằng diện tích tam giác A'B'C' lớn hơn hoặc bằng diện tích tam giác ABC.

b) Gọi X, Y, Z lần lượt là hình chiếu vuông góc của O lên các đường thẳng A'B', B'C', C'A'. Biết rằng đường tròn ngoại tiếp tam giác XYZ lần lượt cắt lại các đường thẳng A'B', B'C', C'A' tại các điểm X', Y', Z' $(X' \neq X, Y' \neq Y, Z' \neq Z)$ . Chứng minh rằng các đường thẳng AX', BY', CZ' đồng quy.

Câu 4 (5,0 điểm)

Người ta xếp k viên bi vào các ô của một bảng 2024 x 2024 ô vuông sao cho hai điều kiện sau được thỏa mãn: mỗi ô không có quá một viên bi và không có hai viên bi nào được xếp ở hai ô kề nhau (hai ô được gọi là kề nhau nếu chúng có chung một cạnh).

a) Cho k = 2024. Hãy chỉ ra một cách xếp thỏa mãn cả hai điều kiện trên mà khi chuyển bất kì viên bi đã được xếp nào sang một ô tùy ý kề với nó thì cách xếp mới không còn thỏa mãn cả hai điều kiện trên.

b) Tìm giá trị k lớn nhất sao cho với mọi cách xếp k viên bi thỏa mãn hai điều kiện trên ta có thể chuyển một trong số các viên bi đã được xếp sang một ô kề với nó mà cách xếp mới vẫn không có hai viên bi nào được xếp ở hai ô kề nhau.

Để xem đầy đủ đề thi và lời giải chi tiết mời bạn đọc tải tài liệu về.

Xem thêm