Đề thi HSG Toán 12 cấp tỉnh năm 2023

Đề thi HSG Toán 12 cấp tỉnh năm 2023 - 2024 sở GD&ĐT Long An

Trịnh Thị Thu Hiền Ngày: 25-06-2024 Lớp 12

Tải xuống 8 48 0

Tailieumoi.vn xin giới thiệu đề thi học sinh giỏi Toán lớp 12 cấp tỉnh năm 2023 - 2024 sở GD&ĐT Long An có lời giải chi tiết. Hi vọng với bộ tài liệu này các em ôn luyện, củng cố kiến thức, rèn luyện kĩ năng làm bài thật tốt để bước bài kì thi HSG sắp tới.

Đề thi HSG Toán 12 cấp tỉnh năm 2023 - 2024 sở GD&ĐT Long An

Một số câu hỏi có trong đề thi:

Câu 1 (5,0 điểm):

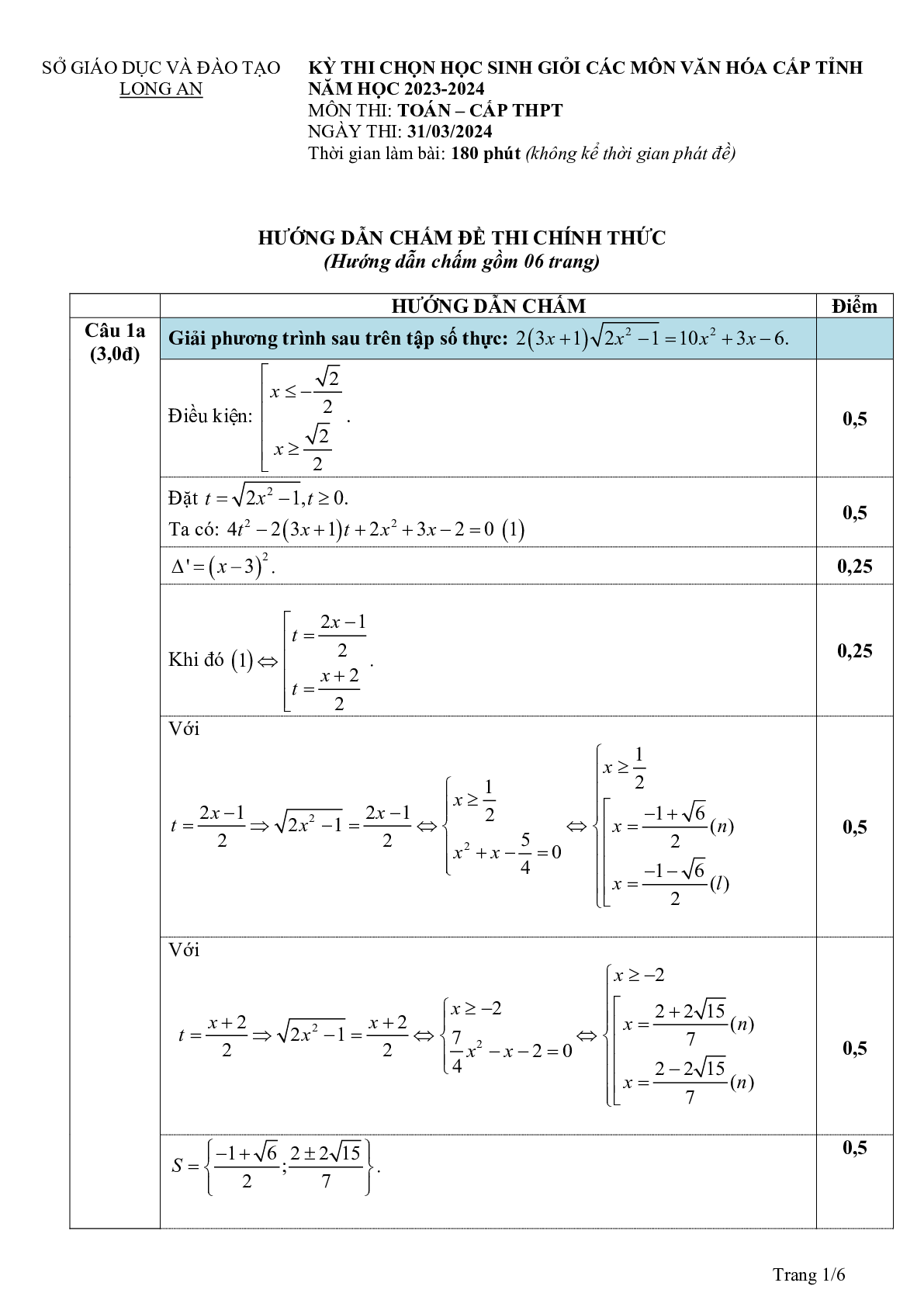
a) Giải phương trình sau trên tập số thực: $2 (3 x + 1) \sqrt{2 x^{2} - 1} = 10 x^{2} + 3 x - 6$ .

b) Giải hệ phương trình $\{\begin{cases} x \sqrt{x} - 12 \sqrt{y} + 3 \sqrt{x y} = y \sqrt{y} - 25 \\ \sqrt{x} + 2 y = x + \sqrt{x y} + 6 \end{cases} (x, y \in ℝ) .$

Câu 2 (5,0 điểm):

a) Cho tam giác ABC có độ dài ba cạnh $B C = a, C A = b, A B = c, \overset{⏜}{A} = 60 °$ và $\frac{b - c}{a + c} = 2 (\cos B - 1) .$ Tính số đo góc B .

b) Trong mặt phẳng với hệ tọa độ Oxy , cho hình thang vuông ABCD vuông tại A và D , có CD = 2AD = 2AB. Gọi M = (2; 4) là điểm thuộc cạnh AB sao cho AB = 3AM. Điểm N thuộc cạnh BC sao cho tam giác DMN cân tại M. Phương trình đường thẳng MN là $2 x + y - 8 = 0$ . Tìm tọa độ đỉnh B của hình thang ABCD biết D thuộc đường thẳng $d : x + y = 0$ và điểm A thuộc đường thẳng : $d' : 3 x + y - 8 = 0$ .

Câu 3 (4,0 điểm): Cho dãy số $(u_{n}) = \{\begin{cases} u_{1} = 1 \\ u_{n + 1} = \frac{u_{n}}{u_{n} + 2}, \forall n \in ℕ * \end{cases}$

a) Dãy số $(u_{n})$ là dãy số tăng hay dãy số giảm? Vì sao?

b) Tìm công thức số hạng tổng quát của dãy số $(u_{n})$ .

Câu 1 (5,0 điểm):
a) Giải phương trình sau trên tập số thực: ( ) 2 2
2 3 1 2 1 10 3 6+ − = + −x x x x .
b) Giải hệ phương trình ( )
12 3 25 ,
2 + 6
x x y xy y y x y
x y x xy
 − + = − ∈ + = +
 .
Câu 2 (5,0 điểm):
a) Cho tam giác ABC có độ dài ba cạnh  0
, , , 60= = = =BC a CA b AB c A và
( )2 1
− = −
+
b c cosB
a c . Tính số đo góc B .
b) Trong mặt phẳng với hệ tọa độ Oxy , cho hình thang vuông ABCD vuông tại A
và D , có 2 2= =CD AD AB . Gọi ( )2; 4M là điểm thuộc cạnh AB sao cho
3=AB AM . Điểm N thuộc cạnh BC sao cho tam giác DMN cân tại M .
Phương trình đường thẳng MN là 2 8 0+ − =x y . Tìm tọa độ đỉnh B của hình
thang ABCD biết D thuộc đường thẳng : 0+ =d x y và điểm A thuộc đường
thẳng : 3 8 0′ + − =d x y .
Câu 3 (4,0 điểm):
Cho dãy số
1
*
1
1
( ) : , .
2
n n
n
n
u
u u
u n
u
+
=

 = ∀ ∈ +

a) Dãy số ( )nu là dãy số tăng hay dãy số giảm? Vì sao?
b) Tìm công thức số hạng tổng quát của dãy số ( )nu