Tailieumoi.vn xin giới thiệu đề thi học sinh giỏi Toán lớp 12 cấp tỉnh năm 2023 - 2024 sở GD&ĐT An Giang có lời giải chi tiết. Hi vọng với bộ tài liệu này các em ôn luyện, củng cố kiến thức, rèn luyện kĩ năng làm bài thật tốt để bước bài kì thi HSG sắp tới.

Đề thi HSG Toán 12 cấp tỉnh năm 2023 - 2024 sở GD&ĐT An Giang

Một số câu hỏi có trong đề thi:

Câu 1: (3,0 điểm) Cho bảng các tích của 𝑚 số lẻ và 𝑛 số chẵn. Tính tổng của các tích trong
bảng sau
1 3 5 ... 2𝑚 − 1
2 2 6 10 ... 4𝑚 − 2
4 4 12 20 ... 8𝑚 − 4
.
.
.
.
.
.
2𝑛 2𝑛 6𝑛 10𝑛 ... 2𝑛(2𝑚 − 1)
Câu 2: (3,0 điểm) Cho cấp số cộng có 20 số hạng 𝑎1; 𝑎2; ... ; 𝑎20. Đặt 𝐴 = 𝑎1 + 𝑎3 + ⋯ +
𝑎19 và 𝐵 = 𝑎2 + 𝑎4 + ⋯ + 𝑎20. Biết 𝐵 − 𝐴 = 110; √𝐵 − √𝐴 = √10. Tìm số hạng đầu tiên
và số hạng thứ 20 của cấp số.
Câu 3: (2,0 điểm) Một hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ có ba kích thước
là 𝐴𝐵 = 1𝑐𝑚; 𝐴𝐷 = 2 𝑐𝑚; 𝐴𝐴′ = 2𝑐𝑚 và đường chéo 𝐷𝐵′. Tìm các đường
đi ngắn nhất để một con chuột bò trên các cạnh hoặc đường chéo, xuất phát
từ đỉnh 𝐴 đi qua tất cả các đỉnh đúng một lần và kết thúc tại đỉnh 𝐶′.
Câu 4: (2,0 điểm) Cho tứ diện 𝑂𝐴𝐵𝐶 có 𝑂𝐴; 𝑂𝐵; 𝑂𝐶 đôi một vuông góc
nhau, 𝑂𝐴 = 𝑎; 𝑂𝐵 = 𝑏; 𝑂𝐶 = 𝑐. Gọi 𝑀, 𝑁 là trọng tâm của các tam giác
𝐴𝐵𝐶, 𝑂𝐵𝐶. Tính độ dài đoạn 𝑂𝑀, 𝐴𝑁 theo 𝑎, 𝑏, 𝑐.
Câu 5: (2,0 điểm) Người ta dùng bốn màu: Xanh, Đỏ, Tím, Vàng để sơn 15 thanh chắn lắp
song song và cách đều nhau của một ngôi trường mẫu giáo. Hỏi có
bao nhiêu cách sơn sao cho hai thanh kề nhau thì khác màu và hai
thanh đối xứng nhau qua thanh chính giữa thì cùng màu?Câu 1: (3,0 điểm) Cho bảng các tích của 𝑚 số lẻ và 𝑛 số chẵn. Tính tổng của các tích trong bảng sau

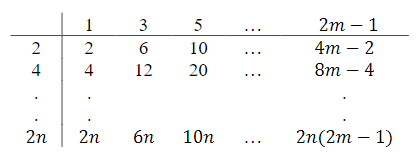
Câu 2: (3,0 điểm) Cho cấp số cộng có 20 số hạng 𝑎₁; 𝑎₂; ... ; 𝑎₂₀. Đặt 𝐴 = 𝑎₁ + 𝑎₃ + ⋯ + 𝑎₁₉ và 𝐵 = 𝑎₂ + 𝑎₄ + ⋯ + 𝑎₂₀. Biết 𝐵 − 𝐴 = 110; $\sqrt{B}$ − $\sqrt{A}=\sqrt{10}$. Tìm số hạng đầu tiên và số hạng thứ 20 của cấp số.

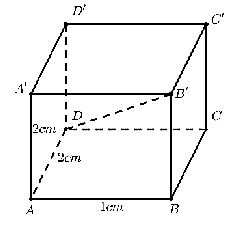
Câu 3: (2,0 điểm) Một hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ có ba kích thước là 𝐴𝐵 = 1𝑐𝑚; 𝐴𝐷 = 2 𝑐𝑚; 𝐴𝐴′ = 2𝑐𝑚 và đường chéo 𝐷𝐵′. Tìm các đường đi ngắn nhất để một con chuột bò trên các cạnh hoặc đường chéo, xuất phát từ đỉnh 𝐴 đi qua tất cả các đỉnh đúng một lần và kết thúc tại đỉnh 𝐶′.

Câu 4: (2,0 điểm) Cho tứ diện 𝑂𝐴𝐵𝐶 có 𝑂𝐴; 𝑂𝐵; 𝑂𝐶 đôi một vuông góc nhau, 𝑂𝐴 = 𝑎; 𝑂𝐵 = 𝑏; 𝑂𝐶 = 𝑐. Gọi 𝑀, 𝑁 là trọng tâm của các tam giác
𝐴𝐵𝐶, 𝑂𝐵𝐶. Tính độ dài đoạn 𝑂𝑀, 𝐴𝑁 theo 𝑎, 𝑏, 𝑐.

Câu 5: (2,0 điểm) Người ta dùng bốn màu: Xanh, Đỏ, Tím, Vàng để sơn 15 thanh chắn lắp song song và cách đều nhau của một ngôi trường mẫu giáo. Hỏi có bao nhiêu cách sơn sao cho hai thanh kề nhau thì khác màu và hai thanh đối xứng nhau qua thanh chính giữa thì cùng màu?Câu 1: (3,0 điểm) Cho bảng các tích của 𝑚 số lẻ và 𝑛 số chẵn. Tính tổng của các tích trong
bảng sau
1 3 5 ... 2𝑚 − 1
2 2 6 10 ... 4𝑚 − 2
4 4 12 20 ... 8𝑚 − 4
.
.
.
.
.
.
2𝑛 2𝑛 6𝑛 10𝑛 ... 2𝑛(2𝑚 − 1)
Câu 2: (3,0 điểm) Cho cấp số cộng có 20 số hạng 𝑎1; 𝑎2; ... ; 𝑎20. Đặt 𝐴 = 𝑎1 + 𝑎3 + ⋯ +
𝑎19 và 𝐵 = 𝑎2 + 𝑎4 + ⋯ + 𝑎20. Biết 𝐵 − 𝐴 = 110; √𝐵 − √𝐴 = √10. Tìm số hạng đầu tiên
và số hạng thứ 20 của cấp số.
Câu 3: (2,0 điểm) Một hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ có ba kích thước
là 𝐴𝐵 = 1𝑐𝑚; 𝐴𝐷 = 2 𝑐𝑚; 𝐴𝐴′ = 2𝑐𝑚 và đường chéo 𝐷𝐵′. Tìm các đường
đi ngắn nhất để một con chuột bò trên các cạnh hoặc đường chéo, xuất phát
từ đỉnh 𝐴 đi qua tất cả các đỉnh đúng một lần và kết thúc tại đỉnh 𝐶′.
Câu 4: (2,0 điểm) Cho tứ diện 𝑂𝐴𝐵𝐶 có 𝑂𝐴; 𝑂𝐵; 𝑂𝐶 đôi một vuông góc
nhau, 𝑂𝐴 = 𝑎; 𝑂𝐵 = 𝑏; 𝑂𝐶 = 𝑐. Gọi 𝑀, 𝑁 là trọng tâm của các tam giác
𝐴𝐵𝐶, 𝑂𝐵𝐶. Tính độ dài đoạn 𝑂𝑀, 𝐴𝑁 theo 𝑎, 𝑏, 𝑐.
Câu 5: (2,0 điểm) Người ta dùng bốn màu: Xanh, Đỏ, Tím, Vàng để sơn 15 thanh chắn lắp
song song và cách đều nhau của một ngôi trường mẫu giáo. Hỏi có
bao nhiêu cách sơn sao cho hai thanh kề nhau thì khác màu và hai
thanh đối xứng nhau qua thanh chính giữa thì cùng màu?Câu 1: (3,0 điểm) Cho bảng các tích của 𝑚 số lẻ và 𝑛 số chẵn. Tính tổng của các tích trong
bảng sau
1 3 5 ... 2𝑚 − 1
2 2 6 10 ... 4𝑚 − 2
4 4 12 20 ... 8𝑚 − 4
.
.
.
.
.
.
2𝑛 2𝑛 6𝑛 10𝑛 ... 2𝑛(2𝑚 − 1)
Câu 2: (3,0 điểm) Cho cấp số cộng có 20 số hạng 𝑎1; 𝑎2; ... ; 𝑎20. Đặt 𝐴 = 𝑎1 + 𝑎3 + ⋯ +
𝑎19 và 𝐵 = 𝑎2 + 𝑎4 + ⋯ + 𝑎20. Biết 𝐵 − 𝐴 = 110; √𝐵 − √𝐴 = √10. Tìm số hạng đầu tiên
và số hạng thứ 20 của cấp số.
Câu 3: (2,0 điểm) Một hình hộp chữ nhật 𝐴𝐵𝐶𝐷. 𝐴′𝐵′𝐶′𝐷′ có ba kích thước
là 𝐴𝐵 = 1𝑐𝑚; 𝐴𝐷 = 2 𝑐𝑚; 𝐴𝐴′ = 2𝑐𝑚 và đường chéo 𝐷𝐵′. Tìm các đường
đi ngắn nhất để một con chuột bò trên các cạnh hoặc đường chéo, xuất phát
từ đỉnh 𝐴 đi qua tất cả các đỉnh đúng một lần và kết thúc tại đỉnh 𝐶′.
Câu 4: (2,0 điểm) Cho tứ diện 𝑂𝐴𝐵𝐶 có 𝑂𝐴; 𝑂𝐵; 𝑂𝐶 đôi một vuông góc
nhau, 𝑂𝐴 = 𝑎; 𝑂𝐵 = 𝑏; 𝑂𝐶 = 𝑐. Gọi 𝑀, 𝑁 là trọng tâm của các tam giác
𝐴𝐵𝐶, 𝑂𝐵𝐶. Tính độ dài đoạn 𝑂𝑀, 𝐴𝑁 theo 𝑎, 𝑏, 𝑐.
Câu 5: (2,0 điểm) Người ta dùng bốn màu: Xanh, Đỏ, Tím, Vàng để sơn 15 thanh chắn lắp
song song và cách đều nhau của một ngôi trường mẫu giáo. Hỏi có
bao nhiêu cách sơn sao cho hai thanh kề nhau thì khác màu và hai
thanh đối xứng nhau qua thanh chính giữa thì cùng màu?

Để xem đầy đủ đề thi và lời giải chi tiết mời bạn đọc tải tài liệu về.