Tailieumoi.vn xin giới thiệu tài liệu Trắc nghiệm Toán lớp 6 Chương 3: Hình học trực quan. Các hình phẳng trong thực tiễn sách Chân trời sáng tạo. Tài liệu gồm 16 câu hỏi trắc nghiệm chọn lọc có đáp án với đầy đủ các mức độ nhận biết, thông hiểu, vận dụng. Mời các bạn đón xem:
Trắc nghiệm Toán lớp 6 Chương 3: Hình học trực quan. Các hình phẳng trong thực tiễn
Phần 1. Trắc nghiệm Chương 3: Hình học trực quan. Các hình phẳng trong thực tiễn
Câu 1. Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì diện tích của nó bằng bao nhiêu?
A. 18 cm2
B. 36 cm2
C. 72 cm2
D. 288 cm2
Trả lời:
Nửa chu vi hình chữ nhật là:
36:2 = 18(cm)
Chiều dài hình chữ nhật là:
18:(2 + 1).2 = 12(cm)
Chiều rộng hình chữ nhật là:
18 – 12 = 6(cm)
Diện tích hình chữ nhật là:
12.6 = 72(cm2)
Đáp án cần chọn là: C
Câu 2. Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.
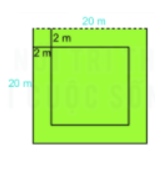
A. 256 m
B. 324 m2
C. 256 m2
D. 324 m
Trả lời:
Phần còn lại để trồng trọt là hình vuông có cạnh:
20 - 2 - 2 = 16 (m)
Diện tích trồng trọt của mảnh vườn là:
16.16 = 256 (m2)
Đáp án cần chọn là: C
Câu 3. Bản thiết kế một hiên nhà được biểu thị ở hình sau. Nếu chi phí làm mỗi 9 dm2 hiên là 103 nghìn đồng thì chi phí của cả hiên nhà sẽ là bao nhiêu?
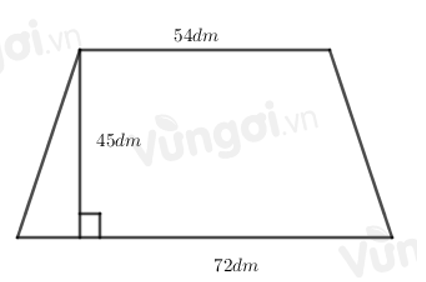
A. 32 445 000 (đồng)
B. 34 225 000 (đồng)
C. 32 455 000 (đồng)
D. 32 544 000 (đồng)
Trả lời:
Diện tích của hiên nhà là: .45.(54 + 72) = 2835 (dm2)
Vậy chi phí của cả hiên là: 2835 : 9 . 103 000 = 32 445 000 (đồng).
Đáp án cần chọn là: A
Câu 4. Trong các hình dưới đây, hình nào là hình bình hành?
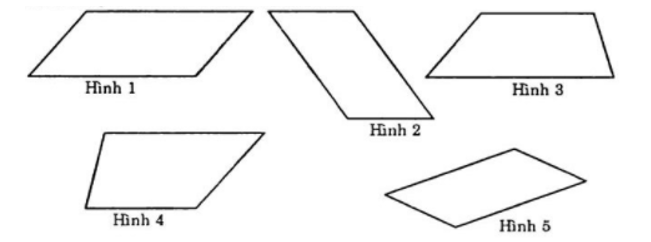
A. Hình 2
B. Hình 2 và hình 3
C. Hình 1, hình 2, hình 5
D. Hình 1, hình 2
Trả lời:
Do hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
=> Các hình là hình bình hành là: Hình 1, hình 2, hình 5.
Đáp án cần chọn là: C
Câu 5. Cho hình bình hành ABCD, cặp cạnh bằng nhau là:
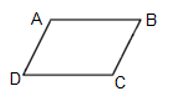
A. AB và AD
B. AD và DC
C. BC và AB
D. DC và AB
Trả lời:
Vì trong hình bình hành hai cặp cạnh đối diện bằng nhau nên DC = AB.
Đáp án cần chọn là: D
Câu 6. Cho hình thoi MPNQ như hình dưới với MN = 8cm; PQ = 6 cm. Diện tích hình thoi MPNQ là:
A. 48 cm2
B. 28 cm2
C. 24 cm
D. 24 cm2
Trả lời:
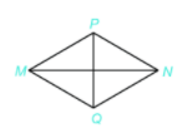
Diện tích hình thoi MPNQ là: 8.6:2 = 24 (cm2)
Đáp án cần chọn là: D
Câu 7. Cho hình thoi MNPQ, biết MP = 5 cm, Chu vi của hình thoi MPNQ là:
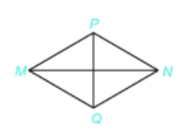
A. 20 cm2
B. 25 cm
C. 20 cm
D. 10 cm
Trả lời:
Chu vi hình thoi MPNQ là: 4.5 = 20 (cm)
Đáp án cần chọn là: C
Câu 8. Một mảnh giấy hình chữ nhật có diện tích 96 cm. Một cạnh có độ dài 12 cm. Tính chu vi của mảnh giấy đó?
A. 8 cm
B. 20 cm
C. 40 cm
D. 80 cm
Trả lời:
Chiều dài cạnh còn lại của mảnh giấy hình chữ nhật là: 96 : 12 = 8 (cm)
Chu vi của mảnh giấy là: 2.(8 + 12) = 40 (cm)
Đáp án cần chọn là: C
Câu 9. Một mảnh vườn hình chữ nhật có chiều dài 25 m. Chiều rộng bằng 15 m. Người ta làm hai lối đi rộng 1 m như hình vẽ. Phần đất còn lại dùng để trồng cây. Tính diện tích đất dùng để trồng cây.
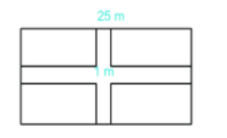
A. 84 m2
B. 336 m2
C. 152 m2
D. 58 m2
Trả lời:
Chiều rộng của mảnh vườn là: (m)
Từ hình vẽ ta thấy diện tích đất trồng cây là 4 mảnh đất hình chữ nhật nhỏ có kích thước như nhau.
Chiều dài của các mảnh đất đó là: (25 - 1) : 2 = 12 (m)
Chiều rộng của các mảnh đất đó là: (15 - 1) : 2 = 7 (m)
Vậy diện tích đất để trồng cây là: 4.7.12 = 336 (m2)
Đáp án cần chọn là: B
Câu 10. Một mảnh vườn có hình dạng như hình dưới đây. Tính diện tích mảnh vườn.
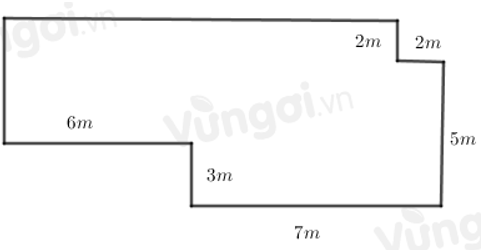
A. 91 m2
B. 18 m2
C. 87 m2
D. 69 m2
Trả lời:
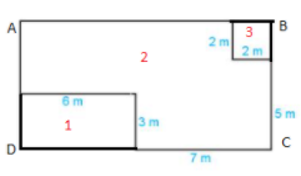
Ta thấy tổng diện tích của hình 1, hình 2, hình 3 bằng tổng diện tích của hình chữ nhật ABCD
Chiều dài DC của hình chữ nhật ABCD là: 7 + 6 = 13 (m)
Chiều rộng của hình chữ nhật ABCD là: 2 + 5 = 7 (m)
Diện tích hình chữ nhật ABCD là: 13.7 = 91 (m2)
Hình 1 là hình chữ nhật có chiều dài 6 m và chiều rộng 3 m nên diện tích hình 1 là:
6.3 = 18 (m2)
Hình 3 là hình vuông có cạnh bằng 2 m nên diện tích hình 3 là: 2.2 = 4 (m2)
Vậy diện tích mảnh vườn bằng cần tìm bằng diện tích hình 2 và bằng:
91 - 18 - 4 = 69 (m2)
Đáp án cần chọn là: D
Câu 11. Quan sát hình thang cân EFGH, góc H của hình thang đó bằng góc nào?
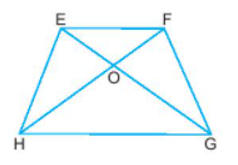
A. Góc E
B. Góc F
C. Góc G
D. Góc O
Trả lời:
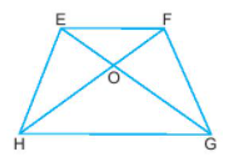
Do góc H và góc G cùng kề đáy HG của hình thang EFGH nên:
Góc H bằng góc G.
Đáp án cần chọn là: C
Câu 12. Cho hình thang cân ABCD, có BC = 3 cm. Chọn khẳng định đúng
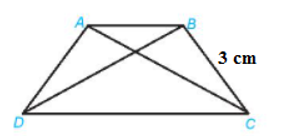
A. AB = 3cm
B. AD = 3cm
C. DC = 3cm
D. AC= 3cm
Trả lời:
Hình thang cân ABCD có AD và BC là hai cạnh bên nên: AD = BC = 3 cm.
Đáp án cần chọn là: B
Câu 13.
Trong các hình sau, hình nào là hình bình hành?
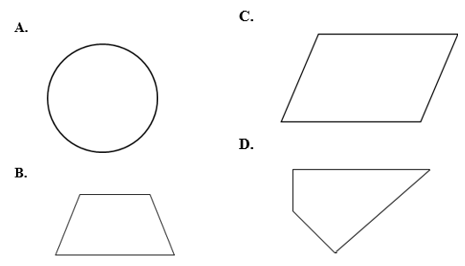
Trả lời:
Quan sát các hình đã cho ta thấy hình A là hình tròn; hình B là hình thang, hình D là tứ giác ; hình C có hai cặp cạnh đối diện song song và bằng nhau nên hình C là hình bình hành.
Vậy trong các hình đã cho, hình C là hình bình hành.
Câu 14.
Trong các hình sau, hình nào là hình thoi?
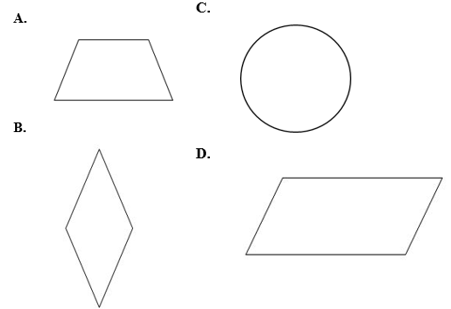
Trả lời:
Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.
Vậy trong các hình đã cho, hình B là hình thoi.
Câu 15.
Cho hình vẽ như sau:
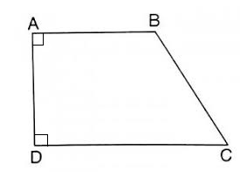
Cạnh AB song song với cạnh nào dưới đây?
A. BC
B. DC
C. AD
Trả lời:
Quan sát hình vẽ ta thấy cạnh AB song song với cạnh DC.
Câu 16. Điền số thích hợp vào ô trống:
Hình chữ nhật MNPQ có.......cặp cạnh vuông góc với nhau.
Trả lời:
Trong hình chữ nhật MNPQ có:
MN vuông góc với MQ; MN vuông góc với NP;
PQ vuông góc với PN; PQ vuông góc với QM.
Vậy hình chữ nhật MNPQ có 4 cặp cạnh vuông góc với nhau.
Đáp án đúng điền vào ô trống là 4.
Phần 2. Lý thuyết Chương 3: Hình học trực quan và hình phẳng trong thực tiễn
1. Hình vuông
Hình vuông có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Bốn góc bằng nhau và bằng góc vuông.
+ Hai đường chéo của hình vuông bằng nhau.
Ví dụ:
Hình vuông ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA.
- Bốn góc ở các đỉnh A, B, C, D là góc vuông.
- Hai đường chéo bằng nhau: AC = BD.
Cách vẽ hình vuông
Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng a (cm).
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = a (cm).
Bước 3: Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = a (cm).
Bước 4: Nối C với D ta được hình vuông ABCD.
2. Tam giác đều
Tam giác đều có:
+ Ba đỉnh.
+ Ba cạnh bằng nhau.
+ Ba góc ở ba đỉnh bằng nhau.
Ví dụ:
Tam giác đều ABC có:
- Ba đỉnh A, B, C.
- Ba cạnh bằng nhau: AB = BC = CA.
- Ba góc đỉnh A, B, C bằng nhau.
Cách vẽ tam giác đều
Cách vẽ tam giác đều cạnh a (cm) bằng thước và compa:
Bước 1: Dùng thước vẽ đoạn thẳng AB = a (cm).
Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.
Bước 3: Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.
Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC.
Ta được tam giác ABC đều cạnh a (như hình vẽ).
3. Lục giác đều
Hình lục giác đều có sáu đỉnh, sáu cạnh bằng nhau, sáu góc ở các đỉnh bằng nhau, ba đường chéo chính bằng nhau.
Ví dụ:
Lục giác đều ABCDEF có:
- Sáu đỉnh A, B, C, D, E, F.
- Sáu cạnh bằng nhau: AB = BC = CD = DE = EF.
- Sáu góc đỉnh A, B, C, D, E, F bằng nhau.
- Ba đường chéo chính bằng nhau AD = BE = CF.
4. Hình chữ nhật
Hình chữ nhật có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Bốn góc ở các đỉnh bằng nhau và bằng góc vuông.
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Ví dụ:
Hình chữ nhật ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
AC = BD và OA = OC; OB = OD.
Cách vẽ hình chữ nhật
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm.
Bước 4. Vẽ đoạn thẳng CD. Ta được hình chữ nhật ABCD.
5. Hình thoi
Hình thoi có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Hai cặp cạnh đối diện song song với nhau.
+ Hai đường chéo vuông góc với nhau.
Ví dụ:
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA;
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
Cách vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB = 5 cm và AC = 8 cm.
Hướng dẫn giải
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm.
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA. Ta được hình thoi ABCD (như hình vẽ).
6.Hình bình hành
Hình bình hành có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Hai cặp góc đối diện bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Ví dụ:
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C; góc đỉnh B bằng góc đỉnh D.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.
Cách vẽ hình bình hành
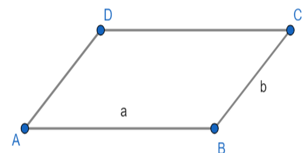
Hình bình hành ABCD có hai cạnh là a và b.
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = b (cm).
Bước 3: Vẽ đường thẳng đi qua A và song song với cạnh BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
7.Hình thang cân
Hình thang cân có:
+ Hai cạnh đáy song song.
+ Hai cạnh bên bằng nhau.
+ Hai góc kề một đáy bằng nhau.
+ Hai đường chéo bằng nhau.
Ví dụ:
Hình thang cân EFGH có:
- Hai cạnh đáy song song: EF song song với GH.
- Hai cạnh bên bằng nhau: EH = FG.
- Hai góc kề một đáy bằng nhau: góc đỉnh E bằng góc đỉnh F, góc đỉnh G bằng góc đỉnh H.
- Hai đường chéo bằng nhau: EG = FH.
Cách gấp hình thang cân
Bước 1: Gấp đôi một tờ giấy hình chữ nhật.
Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3: Mở tờ giấy ra ta được một hình thang cân.
8.Chu vi và diện tích hình chữ nhật
Cho hình chữ nhật có chiều dài là a, chiều rộng là b (như hình vẽ).
Chu vi của hình chữ nhật là: P = (a + b) . 2
Diện tích của hình chữ nhật là: S = a . b
9. Chu vi và diện tích của hình vuông
Cho hình vuông có độ dài một cạnh bằng a (như hình vẽ).
Chu vi hình vuông là: P = 4a.
Diện tích hình vuông là: S = a . a = a2.
10. Chu vi và diện tích của hình tam giác
Cho tam giác có độ dài ba cạnh lần lượt là a, b, c và chiều cao tương ứng với cạnh a có độ dài là h (như hình vẽ).
Chu vi hình hình tam giác là: P = a + b + c.
Diện tích hình tam giác là: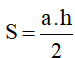 
.
11. Chu vi và diện tích của hình thang
Cho hình thang có độ dài bốn cạnh là a, b, c, d và đường cao h (như hình vẽ).
Chu vi của hình thang là: P = a + b + c + d
Diện tích của hình thang là: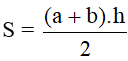 
.
12. Chu vi và diện tích hình bình hành
Cho hình bình hành có độ dài hai cạnh là a và b, chiều cao tương ứng với một cạnh a có độ dài là h (như hình vẽ).
Chu vi hình bình hành là: P = 2(a + b).
Diện tích hình bình hành là: S = a . h
13. Chu vi và diện tích hình thoi
Cho hình thoi có độ dài một cạnh là a, độ dài hai đường chéo của hình thoi là m và n.
Chu vi của hình thoi là: P = 4a.
Diện tích của hình thoi là: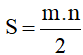 
.
14. Chu vi và diện tích của một số hình trong thực tiễn
a) Tính chu vi của một số hình trong thực tiễn:
Chu vi của một hình bằng tổng độ dài các đoạn thẳng bao quanh hình đó.
b) Tính diện tích của một số hình trong thực tiễn:
− Nếu hình đã cho là các hình đã biết công thức như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, … thì ta áp dụng công thức và tính.
− Nếu hình đã cho không phải các hình đã biết công thức tính thì ta chia hình đã cho thành các hình đã biết công thức tính như: Hình tam giác, hình vuông, hình chữ nhật, hình thoi, …
Xem thêm các bài trắc nghiệm Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Chương 2: Số nguyên
Trắc nghiệm Chương 3: Hình học trực quan và hình học phẳng trong thực tiễn
Trắc nghiệm Chương 4: Một số yếu tố thống kê
Trắc nghiệm Chương 6: Số thập phân
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
