Với giải bài tập Toán lớp 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia chi tiết bám sát nội dung sgk Toán 6 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia
Video giải Toán 6 Bài 3: Hai đường thẳng cắt nhau, song song. Tia – Chân trời sáng tạo
A. Các câu hỏi trong bài
Giải Toán 6 trang 77 Tập 2 Chân trời sáng tạo
Lời giải:
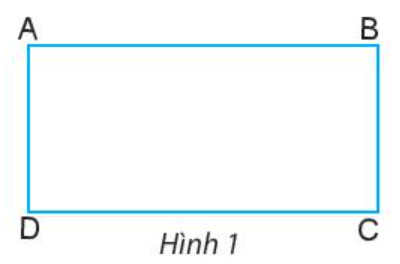
Trong Hình 1:
- Số điểm chung của hai đường thẳng AB và AD:
+ Đường thẳng AB có chứa hai điểm A và B.
+ Đường thẳng AD có chứa hai điểm A và D.
Do đó, hai đường thẳng AB và AD có một điểm chung là A.
Số điểm chung của hai đường thẳng AB và DC:
+ Đường thẳng AB có chứa hai điểm A và B.
+ Đường thẳng DC có chứa hai điểm D và C.
Do đó, hai đường thẳng AB và DC không có điểm chung.
Vậy hai đường thẳng AB và AD có một điểm chung là A và hai đường thẳng AB và DC không có điểm chung.
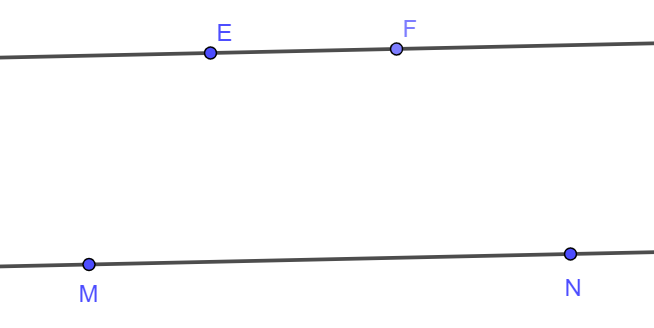
Thực hành trang 77 Toán lớp 6 Tập 2: Cho đường thẳng MN như hình bên.
Hãy vẽ hình trong các trường hợp sau:
a) Đường thẳng CD cắt đường thẳng MN;
b) Đường thẳng EF song song với đường thẳng MN.
Lời giải:
a) Đường thẳng CD cắt đường thẳng MN nên hai đường thẳng này có một điểm chung.
Chẳng hạn: vẽ hai đường thẳng CD và MN cắt nhau tại điểm A.
Cách vẽ:
Bước 1: Vẽ đường thẳng MN bất kỳ.
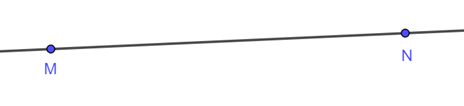
Bước 2: Lấy điểm A bất kỳ thuộc đường thẳng MN, giả sử điểm A nằm giữa hai điểm M và N.
Bước 3: Vẽ đường thẳng đi qua A và không trùng với đường thẳng CD.
Ta có đường thẳng CD cắt đường thẳng MN như hình vẽ:
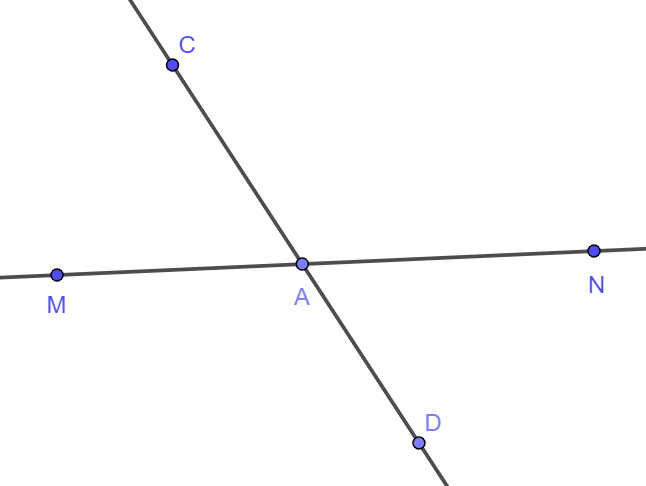
b) Cách vẽ đường thẳng EF song song với đường thẳng MN:
Bước 1: Vẽ đường thẳng MN bất kỳ.
Bước 2: Lấy điểm E nằm ngoài đường thẳng MN.
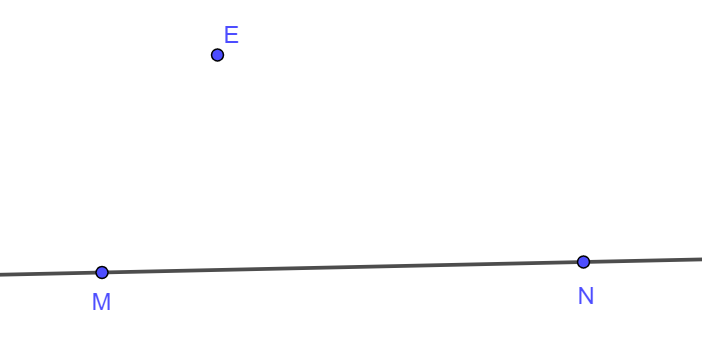
Bước 3: Vẽ đường thẳng đi qua điểm E và song song với đường thẳng MN. Lấy điểm F thuộc đường thẳng vừa vẽ.
Ta được đường thẳng EF song song với đường thẳng MN như hình vẽ:
Giải Toán 6 trang 78 Tập 2 Chân trời sáng tạo
- Hãy tìm hình ảnh tia trong thực tiễn.
Lời giải:
- Hình ảnh của hai đường thẳng song song, cắt nhau trong thực tiễn:
• Hình ảnh của hai đường thẳng song song trong thực tiễn:
+ Hai đường dây điện.
+ Hai mép bàn hình chữ nhật.
• Hình ảnh hai đường thẳng cắt nhau trong thực tiễn:
Chiều dài và chiều rộng của căn phòng.
- Hình ảnh tia trong thực tiễn:
+ Tia sét.
+ Tia laser.
B. Bài tập
Qua hai điểm A và B phân biệt có
(A) vô số đường thẳng.
(B) chỉ có 1 đường thẳng.
(C) không có đường thẳng nào.
Lời giải:
Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
Do đó, qua hai điểm A và B phân biệt chỉ có 1 đường thẳng đi qua hai điểm đó.
Vậy phương án đúng là (B) chỉ có 1 đường thẳng.
Bài 2 trang 78 Toán lớp 6 Tập 2: Vẽ hình cho các trường hợp sau:
a) Hai đường thẳng p và q cắt nhau tại điểm M.
b) Đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y trong hai trường hợp: m và n cắt nhau, hoặc m và n song song với nhau.
Lời giải:
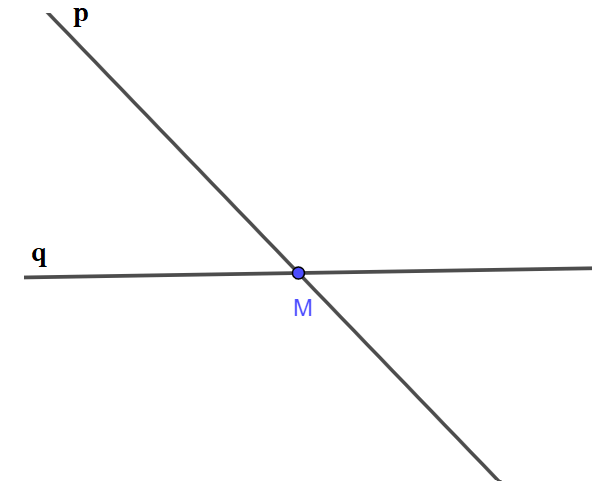
a) Cách vẽ hai đường thẳng p và q cắt nhau tại điểm M:
Cách 1:
- Vẽ đường thẳng p bất kỳ.
- Vẽ đường thẳng q cắt đường thẳng p.
- Lấy điểm M là giao điểm của hai đường thẳng p và q.
Ta có hình vẽ:
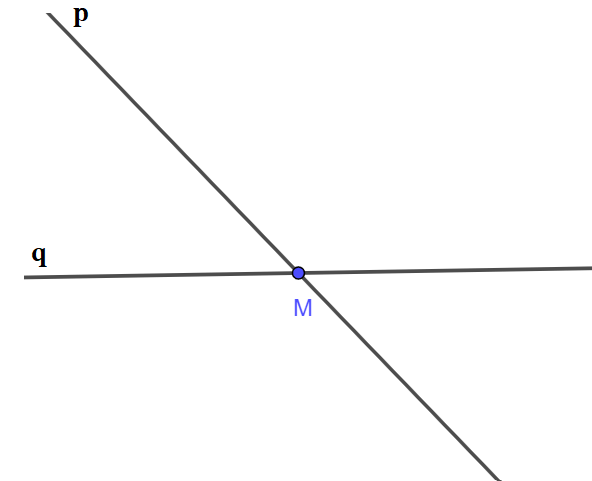
Cách 2:
- Vẽ đường thẳng p bất kỳ.
- Lấy điểm M thuộc đường thẳng p.
- Vẽ đường thẳng q đi qua điểm M và không trùng với đường thẳng p.
Ta có hình vẽ:
b) Vì đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y nên ta sẽ không xét trường hợp ba đường thẳng giao nhau tại một điểm.
Ta xét hai trường hợp còn lại:
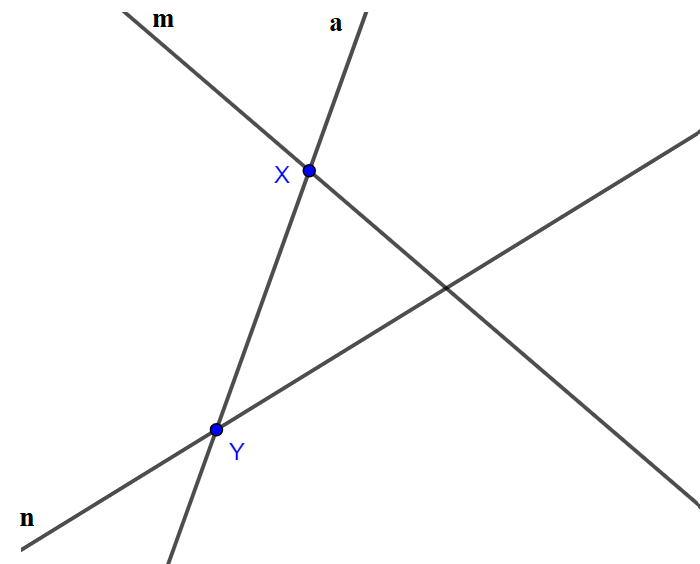
- Trường hợp 1: Đường thẳng m và đường thẳng n cắt nhau. Đường thẳng a cắt hai đường thẳng m và n lần lượt tại điểm X và Y.
* Cách vẽ:
- Vẽ đường thẳng m bất kỳ.
- Vẽ đường thẳng n cắt đường thẳng m.
- Vẽ đường thẳng a cắt hai đường thẳng m và n lần lượt tại hai điểm X và Y.
* Ta có hình vẽ:
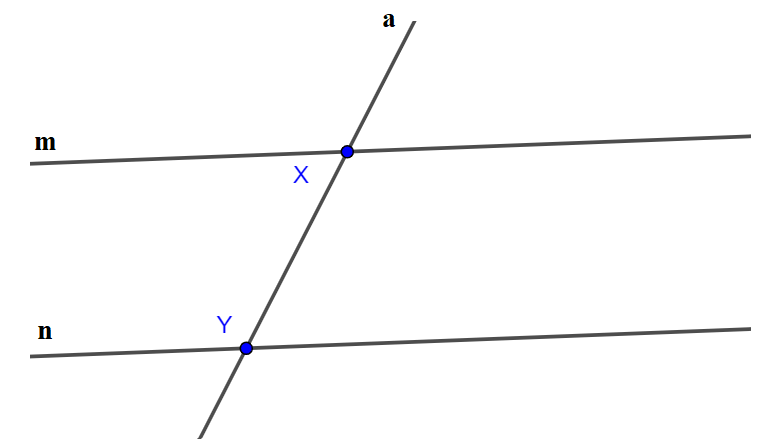
- Trường hợp 2: Đường thẳng m và đường thẳng n song song với nhau. Đường thẳng a cắt hai đường thẳng m và n lần lượt tại điểm X và Y.
* Cách vẽ:
- Vẽ đường thẳng m bất kỳ.
- Vẽ đường thẳng n song song với đường thẳng m.
- Vẽ đường thẳng a cắt hai đường thẳng m và n lần lượt tại hai điểm X và Y.
* Ta có hình vẽ:
Bài 3 trang 78 Toán lớp 6 Tập 2: Đếm số giao điểm tạo bởi ba đường thẳng trong mỗi hình sau:
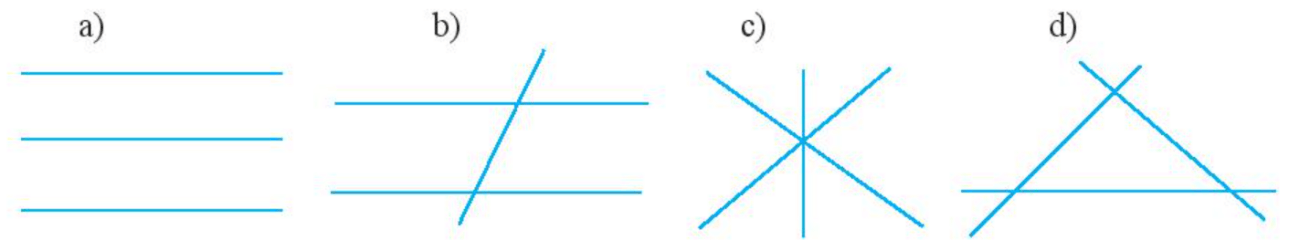
Lời giải:
a) Trong hình a) có ba đường thẳng song song với nhau nên không có giao điểm nào.
b) Đặt các đường thẳng trong hình b) là các đường thẳng a, b, c.
Giả sử đường thẳng a và c cắt nhau tại điểm A, đường thẳng b và c cắt nhau tại điểm B (như hình vẽ).
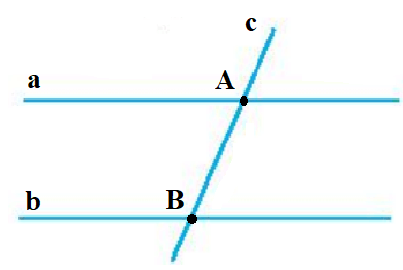
Do đó đường thẳng a và b cắt đường thẳng c lần lượt tại hai điểm A và B.
Vậy trong hình b) có hai giao điểm tạo bởi ba đường thẳng.
c) Đặt các đường thẳng trong hình c) là các đường thẳng m, n, p.
Giả sử ba đường thẳng m, n, p cắt nhau tại điểm M (như hình vẽ).
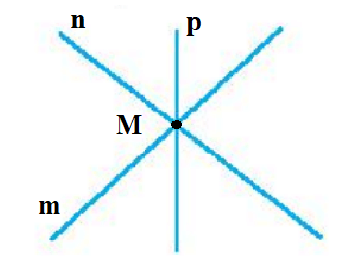
Vậy trong hình c) có một giao điểm tạo bởi ba đường thẳng.
d) Đặt các đường thẳng trong hình d) là các đường thẳng c, d, e.
Giả sử đường thẳng c và e cắt nhau tại điểm C, đường thẳng d và e cắt nhau tại điểm D, đường thẳng c và d cắt nhau tại E (như hình vẽ).
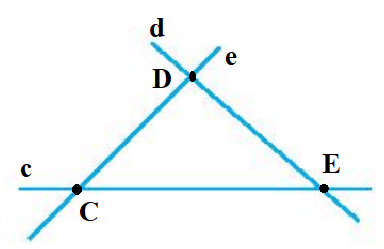
Do đó ba đường thẳng c, d, e đôi một cắt nhau tại các điểm C, D, E.
Vậy trong hình d) có ba giao điểm tạo bởi ba đường thẳng.
Bài 4 trang 78 Toán lớp 6 Tập 2: Kể tên các tia có gốc là M trong hình sau:
Lời giải:
Trên hình vẽ, điểm M nằm trên đường thẳng HF chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc M.
Vậy các tia có gốc là M là: tia MH và tia MF.
Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Ba điểm thẳng hàng. Ba điểm không thẳng
Bài 4: Đoạn thẳng. Độ dài đoạn thẳng
Bài 5: Trung điểm của đoạn thẳng
Lý thuyết Hai đường thẳng cắt nhau, song song. Tia
1. Hai đường thẳng cắt nhau, song song
- Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.
Ví dụ 1. Hai đường thẳng a và b chỉ có một điểm chung là M, ta nói rằng hai đường thẳng a và b cắt nhau (như hình vẽ).
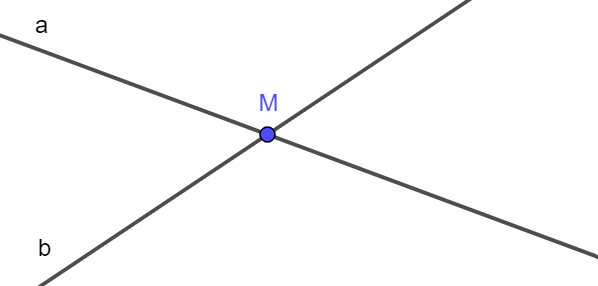
Khi đó, M là giao điểm của hai đường thẳng a và b.
- Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau.
Ví dụ 2. Hai đường thẳng c và d không có điểm chung nào (như hình vẽ).
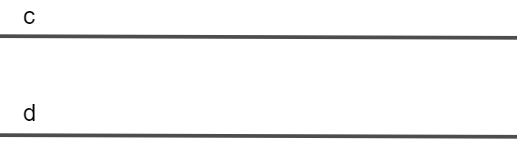
Khi đó, ta nói hai đường thẳng a và b song song với nhau.
Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.
2. Tia
Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.
Chú ý:
- Từ một điểm O kẻ một vạch thẳng về một phía của điểm O để biểu diễn một tia gốc O.
- Nếu A là một điểm tùy ý trên tia Ox, ta có thể gọi tia Ox là tia OA (như hình vẽ).
- Khi viết (đọc) tia, ta phải viết (đọc) gốc của tia trước.
Ví dụ 3. Cho hình vẽ.
Trong hình vẽ có O là điểm gốc.
Ta viết (đọc) gốc của tia trước, viết (đọc) là: tia Ox.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
