Với giải bài tập Toán lớp 6 Bài tập cuối chương 1 chi tiết bám sát nội dung sgk Toán 6 Tập 1 Chân trời sáng tạo giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:

Mục lục Giải bài tập Toán 6 Bài tập cuối chương 1

Video giải Toán 6 Chương 1: Số tự nhiên - Chân trời sáng tạo

A. Các câu hỏi trắc nghiệm

Giải Toán 6 trang 45 Tập 1 Chân trời sáng tạo

Câu 1 trang 45 Toán lớp 6 Tập 1: Gọi X là tập hợp các chữ cái trong từ “thanh”.Cách viết đúng là:

(A) X = {t; h; a; n; h}.

(B) X = {t; h; n};

(C) X= {t; h; a; n}.

(D) X = {t; h; a; n; m}.

Lời giải:

Các chữ cái xuất hiện trong từ “thanh” là: t, h, a, n, h.

Vì các phần tử trong tập hợp chỉ xuất hiện một lần .

Suy ra X = {t, h, a, n}.

Đáp án cần chọn là C.

Câu 2 trang 45 Toán lớp 6 Tập 1: Gọi X là tập hợp các số tự nhiên không lớn hơn 5. Cách viết sai là:

(A) X = {0; 1; 2; 3; 4; 5}.

(B) X = {0; 2; 4; 1; 3; 5}.

(C) X= {x ∈N | x < 5}.

(D) X = {x ∈N| x ≤ 5}. 

Lời giải:

Các số tự nhiện không lớn hơn 5, tức là nhỏ hơn hoặc bằng 5, đó là các số 0, 1, 2, 3, 4, 5.

Khi đó ta viết tập hợp X theo cách liệt kê các phần tử là: 

 X = {0; 1; 2; 3; 4; 5} hoặc X = {0; 2; 4; 1; 3; 5} (thứ tự liệt kê không ảnh hưởng)

Do đó A và B là đúng.

Viết tập hợp X theo cách chỉ ra tính chất đặc trưng: {x ∈ N| x ≤ 5}. Do đó D đúng, C sai.

Đáp án cần chọn là C.

Giải Toán 6 trang 46 Tập 1 Chân trời sáng tạo

Câu 3 trang 46 Toán lớp 6 Tập 1: Cách viết nào sau đây là sai:

(A) a + b = b + a.

(B) ab = ba.

(C) ab + ac = a(b + c).

(D) ab - ac = a(c - b).

Lời giải:

(A) a + b = b + a là tính chất giao hoán của phép cộng nên A đúng.

(B) ab = ba là tính chất giao hoán của phép nhân nên B đúng.

(C) ab + ac = a(b + c) là tính chất phân phối của phép cộng với phép nhân nên C đúng.

(D) Ta có: ab – ac = a(b – c) ≠ a(c – b) do đó D sai.

Đáp án cần chọn là D.

Câu 4 trang 46 Toán lớp 6 Tập 1: Nhẩm xem kết quả phép tính nào dưới đây là đúng:

(A) 11 . 12 = 122.

(B) 13 . 99 = 1 170.

(C) 14 . 99 = 1 386.

(D) 45 . 9 = 415.

Lời giải:

(A)  Ta có 11 . 12 = 132 nên A sai.

(B) Ta có 13.99 = 1 287 nên B sai.

(C) Ta có 14.99 = 1 386 nên C đúng.

(D) Ta có 45.9 = 405 nên D sai.

Đáp án cần chọn là C.

Câu 5 trang 46 Toán lớp 6 Tập 1: ƯCLN(18, 24) là:

(A) 24

(B) 18

(C) 12

(D) 6

Lời giải:

18 = 2.3²; 24 = 2³.3

⇒ƯCLN(18, 24) = 2.3 = 6.

Đáp án cần chọn là D.

Câu 6 trang 46 Toán lớp 6 Tập 1: BCNN(3, 4, 6) là:

(A) 72

(B) 36

(C) 12

(D) 6

Lời giải:

3 = 3; 4 = 2²; 6 = 2.3

⇒ BCNN(3,4,6) = 2².3 = 12.

Đáp án cần chọn là C.

B. Bài tập tự luận

Bài 1 trang 46 Toán lớp 6 Tập 1: Tính giá trị của biểu thức (bằng cách hợp lý nếu có thể).

a) A = 37.173 + 62.173 + 173;

b) B = 72.99 + 28.99 – 900;

c) C = 2³.3 – (1¹⁰ + 15) : 4²;

d) D = 6² : 4.3 + 2.5² – 201⁰.

Lời giải:

a) A = 37.173 + 62.173 + 173

= 37.173 + 62.173 + 173 . 1

= 173.(37 + 62 + 1) 

= 173. 100

= 17 300.

b) B = 72.99 + 28.99 – 900

= 99(72 + 28) – 900

= 99.100 – 900

= 9 900 – 900 

= 9 000.

c) C = 2³.3 – (1¹⁰ + 15):4²

 

 

 

 

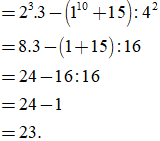
d) D = 6² : 4.3 + 2.5² – 201⁰

 

 

 

 

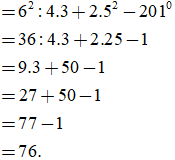
Bài 2 trang 46 Toán lớp 6 Tập 1: Tìm các chữ số x, y biết:

a)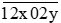  chia hết cho 2; 3 và cả 5.

b)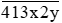  chia hết cho 5 và 9 mà không chia hết cho 2.

Lời giải:

a) Để 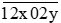 chia hết cho 2 ⇒ Y ∈ { 0; 2; 4; 6; 8}.

Và 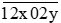 chia hết cho 5 ⇒ Y ∈ {0; 5}.

Do đó y = 0.

Tổng các chữ số của số đã cho là: 1 + 2 + x + 0 + 2 + y = 5 + x.

Để số 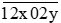 chia hết cho 3 thì 5 + x ⁝ 3 ⇒ 5 + x  ∈ B(3)

Mà 0 ≤ x ≤ 9, x ∈ N ⇒ x ∈ {1; 4; 7}.

Vậy với x ∈ {1; 4; 7} và y = 0  thì 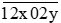 chia hết cho 2; 3 và cả 5.

b) Để 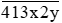 không chia hết cho 2 ⇒ y ∉ {0; 2; 4; 6; 8}

Và 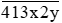 chia hết cho 5 ⇒ Y ∈ {0; 5}..

Do đó y = 5.

Tổng các chữ số của số đã cho là: 4 + 1 + 3 + x + 2 + y = 4 + 1 + 3 + x + 2 + 5 = 15 + x.

Để 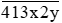 chia hết cho 9 ⇒ 15 + x ⁝ 9 ⇒ 15 +  x  ∈ B(9)

Mà 0 ≤ x ≤ 9, x ∈ N ⇒ x ∈ {3}.

Vậy với x = 3 và y = 5 thì 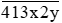 chia hết cho 5 và 9 mà không chia hết cho 2.

Bài 3 trang 46 Toán lớp 6 Tập 1: Viết các tập hợp sau bằng cách liệt kê các phần tử:

a) A = {a ∈ N | 84 ⋮ a; 180⋮a và a > 6}.

b) B = {b ∈N | b ⋮ 12, b ⋮ 15, b ⋮ 18 và 0 < b < 300}.

Lời giải:

a) Ta có: 84 ⋮ a, 180 ⋮ a

Suy ra a ∈ ƯC(84, 180) 

Ta có: 84 = 2².3.7; 180 = 2².3².5

Suy ra ƯCLN(84, 180) = 2².3 = 12

ƯC(84, 180) = Ư(12) = {1; 2; 3; 4; 6; 12}

Mà a > 6 nên a = 12.

Vậy A = {12}.

b) Vì b ⋮ 12, b ⋮ 15, b ⋮ 18 nên b ∈ BC(12, 15, 18)

Ta có: 12 = 2².3; 15= 3.5; 18 = 2.3²

Suy ra BCNN(12, 15, 18) = 2².3².5 = 180.

B(180) = {0; 180; 360; 540; …}.

Khi đó BC(12, 15, 18) = B(180) = {0; 180; 360; 540; …}.

Mà 0 < b < 300  nên b = 180.

Vậy B = {180}.

Bài 4 trang 46 Toán lớp 6 Tập 1: Trong dịp "Hội xuân 2020", để gây quỹ giúp đỡ các bạn học sinh có hoàn cảnh khó khăn, lớp 6A bán hai mặt hàng (như bảng ở cột bên) với mục tiêu số tiền lãi thu được là 500 000 đồng.

Trong thực tế các bạn đã bán được số lượng hàng như sau: trà sữa bán được 93 li, dừa bán được 64 quả.  

Hỏi lớp 6A đã thu được bao nhiêu tiền lãi? Lớp 6A có hoàn thành mục tiêu đã đề ra không?

Lời giải:

Số tiền lớp 6A bỏ ra để nhập hàng là:

100 . 16 500 + 70 . 9 800 = 2 336 000 (đồng)

Số tiền lớp 6A bán được là:

93.20 000 + 64.15 000 = 2 820 000 (đồng)

Số tiền lãi lớp 6A thu được là:

2 820 000 - 2 336 000 = 484 000 (đồng) < 500 000 (đồng)

Vậy: Với mục tiêu số tiền lãi thu được là 500 000 đồng thì lớp 6A không hoàn thành mục tiêu đã đề ra.

Bài 5 trang 46 Toán lớp 6 Tập 1: Thực vật được cấu tạo bởi các tế bào. Tế bào lớn lên đến một kích thước nhất định thì phân chia ra thành 2 tế bào con. Các tế bào con tiếp tục tăng kích thước và lại phân chia thành 4 tế bào, rồi thành 8 tế bào, ... 

Hãy cho biết số tế bào con có được sau lần phân chia thứ tư, thứ năm, thứ sáu từ một tế bào ban đầu.

Lời giải:

Lần 1: Phân chia thành 2 tế bào con

Lần 2: Phân chia thành 4 tế bào con. Suy ra  4 = 2²

Lần 3: Phân chia thành 8 tế bào con. Suy ra 8 = 2³

Ta nhận thấy các tế bào phân chia theo lũy thừa của cơ số 2.

Vậy:

Số tế bào con có được sau lần phân chia thứ tư là: 2⁴ = 16 tế bào.

Số tế bào con có được sau lần phân chia thứ năm là: 2⁵ = 32 tế bào.

Số tế bào con có được sau lần phân chia thứ sáu là: 2⁶ = 64 tế bào.

Bài 6 trang 46 Toán lớp 6 Tập 1: Huy chơi trò xếp 36 que tăm thành những hình giống nhau như các hình dưới đây. Trong mỗi trường hợp a, b, c, d, Huy xếp được bao nhiêu hình như vậy?

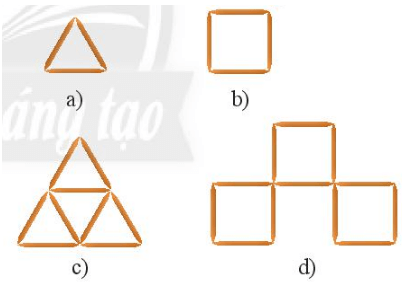
Lời giải:

a) Ở trường hợp a, Huy dùng 3 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 3 = 12 hình.

b) Ở trường hợp b, Huy dùng 4 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 4 = 9 hình.

c) Ở trường hợp c, Huy dùng 9 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 9 = 4 hình.

d) Ở trường hợp d, Huy dùng 12 que tăm để xếp được 1 hình.

Vậy với 36 que tăm thì Huy xếp được số hình là: 36 : 12 = 3 hình.

Bài 7 trang 46 Toán lớp 6 Tập 1: a) Hoàn thiện bảng sau vào vở.

a	8	24	140
b	10	28	60
ƯCLN(a, b)	?	?	?
BCNN(a, b)	?	?	?
ƯCLN(a,b) . BCNN(a, b)	?	?	?
a.b	?	?	?

b) Nhận xét về tích

ƯCLN(a, b) . BCNN(a, b) và tích a . b.

Lời giải:

a) 

+) Ta có: 8 = 2³, 10 = 2.5

⇒ƯCLN(8, 10) = 2

⇒BCNN(8, 10) = 2³.5 = 40.

⇒ƯCLN(8, 10).BCNN(8, 10) = 2.40 = 80.

+) 24 = 2³.3, 28 = 2².7

⇒ƯCLN(24, 28) = 2² = 4

⇒BCNN(24, 28) = 2³.3.7  = 168.

⇒ƯCLN(24, 28).BCNN(24, 28) = 4.168 = 672

+) 140 = 2².5.7; 60 = 2².3.5

⇒ƯCLN(140, 60) = 2².5 =20

⇒BCNN(140, 60) = 2².3.5.7 = 420.

⇒ƯCLN(140, 60).BCNN(140, 60) = 20.420 = 8 400.

Ta hoàn thiện bảng sau:

a	8	24	140
b	10	28	60
ƯCLN(a, b)	2	4	20
BCNN(a, b)	40	168	420
ƯCLN(a,b) . BCNN(a, b)	80	672	8 400
a.b	80	672	8 400

b) Dựa vào bảng vừa hoàn thành ta có nhận xét sau: 

ƯCLN(a, b) . BCNN(a, b) = a . b.

Giải Toán 6 trang 47 Tập 1 Chân trời sáng tạo

Bài 8 trang 47 Toán lớp 6 Tập 1: Nhóm các bạn lớp 6B cần chia 48 quyển vở, 32 chiếc thước kẻ và 56 chiếc bút chì vào trong các túi quà để mang tặng các bạn ở trung tâm trẻ mồ côi sao cho số quyển vở, thước kẻ và bút bi ở mỗi túi đều như nhau. Tính số lượng túi quà nhiều nhất mà nhóm các bạn có thể chia được. Khi đó, số lượng vở, thước kẻ, bút chì trong mỗi túi là bao nhiêu?

Lời giải:

Số lượng túi quà nhiều nhất mà nhóm các bạn có thể chia được là ước chung lớn nhất của 48, 32 và 56.

Ta có: 48 = 2⁴.3; 32 = 2⁵; 56 = 2³.7

 ƯCLN(48, 32, 56) = 2³ = 8.

Vậy số lượng túi quà nhiều nhất mà nhóm có thể chia được là 8 túi.

Khi đó, số lượng vở trong mỗi túi là 48:8 = 6 quyển;

            Số lượng thước kẻ trong mỗi túi là 32:8 = 4 cái;

            Số lượng bút chì trong mỗi túi là: 56:8 = 7 cái.

Bài 9 trang 47 Toán lớp 6 Tập 1:

TOÁN VÀ THƠ

Trung thu gió mát trăng trong

Phố phường đông đúc, đèn lồng sao sa

Rủ nhau đi đếm đèn hoa

Quẩn quanh, quanh quẩn biết là ai hay

Kết năm, chẵn số đèn này

Bảy đèn kết lại còn hai ngọn thừa

Chín đèn thời bốn ngọn dư

Đèn hoa bao ngọn mà ngơ ngẩn lòng.

(Cho biết số đèn từ 600 đến 700 chiếc).

Lời giải:

Phát biểu lại bài toán: Tìm một số từ 600 đến 700 chiếc sao cho số đó chia hết cho 5, chia bảy dư 2 và chia 9 dư 4.

Cộng thêm 5 vào số đó thì số đó chia hết cho 5, 7, 9. Nghĩa là số đó cộng thêm 5 sẽ là bội của 5, 7, 9.

Phân tích 5, 7 và 9 ra thừa số nguyên tố, ta được: 5 = 5, 7 = 7, 9 = 3².

BCNN(5, 7, 9) = 5.7.3² = 315.

BC(5, 7, 9) = B(315) = {0; 315; 630; 945; …}.

Mà số đó nằm trong khoảng từ 600 đến 700 nên số đó là 630.

Vậy số đèn là 630 cái.

Xem thêm các bài giải SGK Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Bài 14: Hoạt động thực hành và trải nghiệm

Bài 1: Số nguyên âm và tập hợp các số nguyên

Bài 2: Thứ tự trong tập hợp số nguyên

Bài 3: Phép cộng và phép trừ hai số nguyên