Với giải bài 4 trang 39 Toán lớp 6 Tập 1 Cánh diều chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Bài 4 trang 39 Toán lớp 6 Tập 1: Tìm chữ số thích hợp ở dấu * để số:
a) 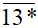 chia hết cho 5 và 9;
chia hết cho 5 và 9;
b) 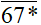 chia hết cho 2 và 3.
chia hết cho 2 và 3.
Lời giải:
a) Vì * là một chữ số trong số 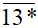 nên * phải là một trong các số: 0; 1; 2; …; 9.
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số 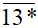 chia hết cho 5 nên
chia hết cho 5 nên 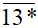 phải có chữ số tận cùng là 0 hoặc 5, hay * phải là 0 hoặc 5.
phải có chữ số tận cùng là 0 hoặc 5, hay * phải là 0 hoặc 5.
Số 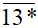 chia hết cho 9 nên tổng các chữ số của số
chia hết cho 9 nên tổng các chữ số của số 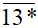 là (1 + 3 + *) = (4 + *) phải là số chia hết cho 9.
là (1 + 3 + *) = (4 + *) phải là số chia hết cho 9.
Thay * lần lượt bằng các số 0; 5 ta được:
+) 4 + 0 = 4 không chia hết cho 9
+) 4 + 5 = 9 chia hết cho 9
Vậy chữ số thích hợp điền vào dấu * để số 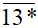 chia hết cho cả 5 và 9 là: 5 hay * = 5.
chia hết cho cả 5 và 9 là: 5 hay * = 5.
b) Số 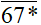 chia hết cho 2 nên
chia hết cho 2 nên 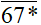 phải có chữ số tận cùng là 0; 2; 4; 6; 8, hay * phải là một trong các số: 0; 2; 4; 6; 8.
phải có chữ số tận cùng là 0; 2; 4; 6; 8, hay * phải là một trong các số: 0; 2; 4; 6; 8.
Số 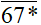 chia hết cho 3 nên tổng các chữ số của số
chia hết cho 3 nên tổng các chữ số của số 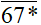 là (6 + 7 + *) = (13 + *) phải là số chia hết cho 3.
là (6 + 7 + *) = (13 + *) phải là số chia hết cho 3.
Thay * lần lượt bằng các số 0; 2; 4; 6; 8 ta được:
+) 13 + 0 = 13 không chia hết cho 3
+) 13 + 2 = 15 chia hết cho 3
+) 13 + 4 = 17 không chia hết cho 3
+) 13 + 6 = 19 không chia hết cho 3
+) 13 + 8 = 21 chia hết cho 3
Vậy các chữ số thích hợp điền vào dấu * để số 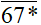 chia hết cho cả 2 và 3 là: 2; 8 hay * = 2 hoặc * = 8.
chia hết cho cả 2 và 3 là: 2; 8 hay * = 2 hoặc * = 8.
Bài tập vận dụng:
Bài 1. Cho các số 104, 627, 3 114, 5 123, 6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Lời giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Bài 2. Chứng minh rằng tích của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
Lời giải:
Gọi 3 số tự nhiên liên tiếp là n; n + 1; n + 2 (với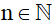 )
)
Tích của ba số tự nhiên liên tiếp là n(n + 1)(n + 2)
Mọi số tự nhiên n khi chia cho 3 có thể nhận số dư là 0, 1, 2.
+ Nếu r = 0 thì n chia hết cho 3. Khi đó n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 1 thì n có dạng n = 3k + 1 (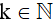 )
)
Ta có: n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 2 thì n có dạng n = 3k + 2 (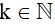 )
)
Khi đó: n + 1 = 3k + 2 + 1 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
Vậy tích của ba số tự nhiên liên tiếp chia hết cho 3.
Xem thêm các bài giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Bài 2 trang 39 Toán lớp 6 Tập 1: Trong các số 2, 3, 5, 9, số nào là ước của n với: a) n = 4 536; ...