Với giải câu hỏi Luyện tập 3 trang 94 Toán lớp 6 Kết nối tri thức với cuộc sống chi tiết được biên soạn bám sát nội dung bài học Toán 6 Bài 20: Chu vi và diện tích của một số tứ giác đã học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
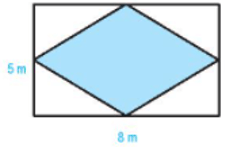
Luyện tập 3 trang 94 Toán lớp 6 Tập 1: Trong mảnh vườn hình chữ nhật có chiều dài 8 m, chiều rộng 5 m, người ta trồng hoa hồng trong một mảnh đất hình thoi như hình bên. Nếu mỗi mét vuông trồng 4 cây hoa thì cần bao nhiêu cây hoa để trồng trên mảnh đất hình thoi đó?
Lời giải:
Dễ thấy độ dài hai đường chéo hình thoi là chiều dài và chiều rộng của hình chữ nhật
Diện tích hình thoi là:
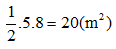
Cần số cây hoa trồng trên mảnh đất hình thoi đó là:
20. 4 = 80 (cây)
Vậy cần 80 cây hoa trồng trên mảnh đất hình thoi đó.
Lý thuyết Chu vi, diện tích hình bình hành, hình thoi.
Hình bình hành:
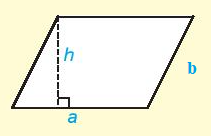
Chu vi: C = 2(a + b).
Diện tích: S = a.h.
Hình thoi:
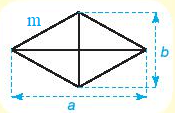
Chu vi: C = 4.m.
Diện tích: S =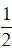 
ab .
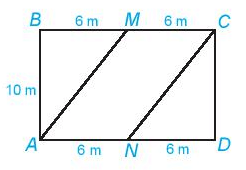
Ví dụ 3. Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m.
a) Người nông dân định làm một tường rào bao quanh khu vườn. Hỏi tường rào đó dài bao nhiêu m?
b) Trên khu vườn nó người nông dân phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành AMCN, cỏ sẽ được trồng ở phần đất còn lại. Tính diện tích trồng hoa và trồng cỏ.
Lời giải
a) Chu vi của khu vườn hình chữ nhật là: 2.(12 + 10) = 2.22 = 44 (m).
Vậy độ dài của tường rào là: 44m.
b) Diện tích trồng hoa là: 6.10 = 60 (m2).
Diện tích khu vườn hình chữ nhật: 12.10 = 120 (m2).
Diện tích trồng cỏ là: 120 – 60 = 60 (m2).
Ví dụ 4. Hình thoi MNPQ có độ dài hai đường chéo 5m và 4m. Diện tích hình thoi MNPQ bằng bao nhiêu?
Lời giải
Diện tích hình thoi MNPQ là: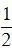 
.5.4 = 10(m2) .
Vậy diện tích hình thoi MNPQ là 10 m2.
Xem thêm các bài giải bài tập Toán lớp 6 sách Kết nối tri thức với cuộc sống hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 6 Kết nối tri thức hay, chi tiết khác:
Bài 19: hình chữ nhật. Hình thoi hình bình hành. Hình thang cân
Bài 20: Chu vi và diện tích của một số tứ giác đã học
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
