Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau:
a) y = x3 – 3x2 + 4 tại điểm có hoành độ x0 = 2;
 Giải bởi Vietjack
Giải bởi Vietjack
a) Từ y = x3 – 3x2 + 4, ta có: y' = (x3)' – (3x2)' + (4)' = 3x2 – 6x.
Do đó y'(2) = 3.22 – 6.2 = 12 – 12 = 0.
y(2) = 23 – 3.22 + 4 = 8 – 12 + 4 = 0.
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x0 = 2 là: y = 0(x – 2) + 0 = 0.
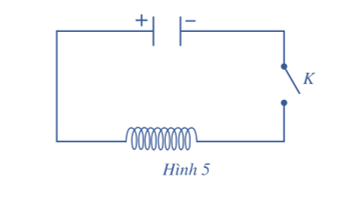
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q(t) = Q0sinωt, trong đó ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức I(t) = q'(t). Cho biết Q0 = 10–8 (C) và ω = 106π (rad/s). Tính cường độ dòng điện tại thời điểm t = 6 (s) (tính chính xác đến 10–5 mA).
Một viên đạn được bắn từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v0 = 196 m/s (bỏ qua sức cản của không khí). Tìm thời điểm mà tốc độ của viên đạn bằng 0. Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy g = 9,8 m/s2)?
Bằng định nghĩa, tính đạo hàm của hàm số y = cosx tại điểm x bất kì.
Bằng định nghĩa, tính đạo hàm của hàm số y = cotx tại điểm x bất kì, x ≠ kπ (k ∈ ℤ).
Bằng định nghĩa, tính đạo hàm của hàm số y = tanx tại điểm x bất kì, (k ∈ ℤ).