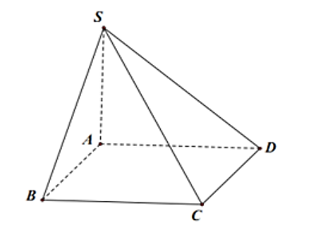
Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình vuông.
 Giải bởi Vietjack
Giải bởi Vietjack
Hình chóp S.ABCD có các mặt bên là các hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác, đáy ABCD là vuông nên hình biểu diễn của đáy ABCD là một hình bình hành. Từ đó ta vẽ được hình biểu diễn của hình chóp S.ABCD như sau:
b) Xác định hình chiếu của điểm A qua phép chiếu song song lên mặt phẳng (SCD) theo phương SB.
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M là điểm thuộc cạnh BC sao cho MB = 2MC.
a) Xác định hình chiếu M' của M qua phép chiếu song song lên mặt phẳng (A'B'C') theo phương AA'.
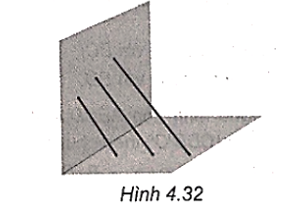
Ba chiếc gậy thẳng được đặt dựa vào tường và đôi một song song với nhau (H.4.32). Giải thích vì sao nếu ba đầu gậy trên tường thẳng hàng thì ba đầu gậy trên mặt sàn cũng thẳng hàng.
Cho hình chóp S.ABCD có đáy ABCD không là hình thang.
a) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Chứng minh rằng bốn điểm A', B', C', D' là bốn đỉnh của một hình bình hành.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A', B', C', D', M', N' lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.
a) Chứng minh rằng hai điểm M' và N' trùng nhau.
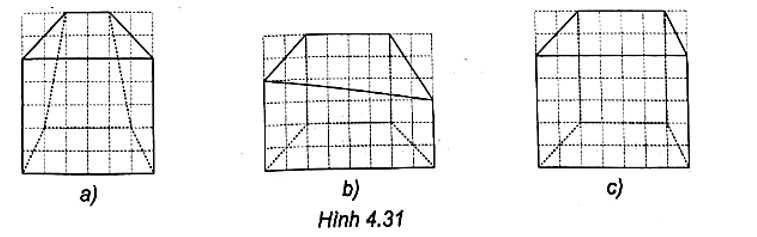
Trong các hình sau, hình nào là hình biểu diễn của hình lăng trụ tứ giác có hai đáy là hình thang?
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Gọi O là giao điểm của AC và BD. Gọi O' là hình chiếu của O qua phép chiếu song song lên mặt phẳng (A'B'C'D') theo phương AA'. Chứng minh rằng O' là giao điểm của A'C' và B'D'.