Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?
 Giải bởi Vietjack
Giải bởi Vietjack
• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90o).
Khi đó, tổng 4 góc nhỏ hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong tứ giác bằng 360o).
• Nếu tứ giác có 3 góc nhọn (nhỏ hơn 90o); 1 góc tù (góc lớn hơn 90o).
Khi đó, tổng 3 góc nhọn nhỏ hơn: 3 . 90o = 270o;
Số đo góc còn lại lớn hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc nhọn.
• Nếu 4 góc tứ giác đều tù (mỗi góc lớn hơn 90o).
Khi đó, tổng 4 góc lớn hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong một tứ giác bằng 360o).
• Nếu tứ giác có 3 góc tù và 1 góc nhọn.
Tổng 3 góc tù lớn hơn: 3.90o = 270o;
Số đo góc còn lại của tứ giác nhỏ hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc tù.
Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.
Khái niệm
Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Định lí tổng các góc của một tứ giác
Tổng số đo các góc của một tứ giác bằng .
Tứ giác ABCD,
Góc nhọn là góc có số đo nhỏ hơn 90o
Góc tù là góc có số đo lớn hơn 90o
Góc vuông là góc có số đo bằng 90o
Bài tập liên quan:
Một tứ giác có nhiều nhất bao nhiêu góc nhọn, bao nhiêu góc tù, bao nhiêu góc vuông?
Cách giải:
• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90°)
Khi đó, tổng 4 góc nhỏ hơn: 4 . 90° = 360° (vô lí vì tổng 4 góc trong tứ giác bằng 360°)
• Nếu tứ giác có 3 góc nhọn (nhỏ hơn 90°); 1 góc tù (góc lớn hơn 90°)
Khi đó, tổng 3 góc nhọn nhỏ hơn: 3 . 90° = 270°
Số đo góc còn lại lớn hơn: 360° – 270° = 90° (thỏa mãn)
Do đó, một tứ giác có thể có nhiều nhất 3 góc nhọn
• Nếu 4 góc tứ giác đều tù (mỗi góc lớn hơn 90°)
Khi đó, tổng 4 góc lớn hơn: 4 . 90° = 360° (vô lí vì tổng 4 góc trong một tứ giác bằng 360°)
• Nếu tứ giác có 3 góc tù và 1 góc nhọn
Tổng 3 góc tù lớn hơn: 3 . 90° = 270°
Số đo góc còn lại của tứ giác nhỏ hơn: 360° – 270° = 90° (thỏa mãn)
Do đó, một tứ giác có thể có nhiều nhất 3 góc tù.
• Nếu 4 góc tứ giác đều vuông (mỗi góc bằng 90°)
Khi đó, tổng 4 góc bằng: 4 . 90° = 360° (thỏa mãn)
Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù, một tứ giác có thể có nhiều nhất 4 góc vuông.
Tham khảo thêm một số tài liệu liên quan:
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
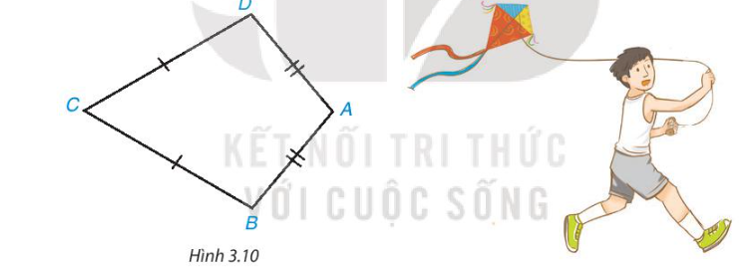
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
Quan sát tứ giác ABCD trong Hình 3.4.
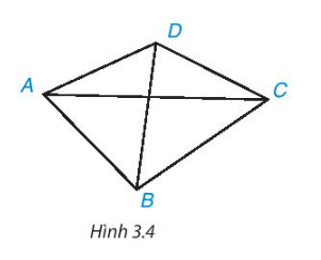
- Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.
- Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.
- Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.
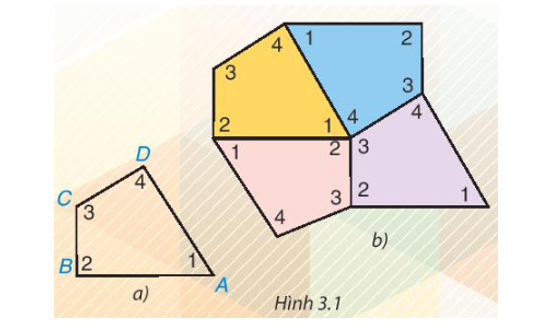
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b
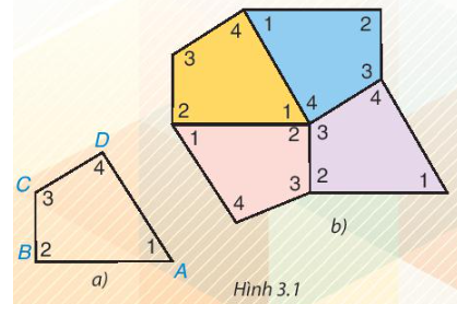
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.
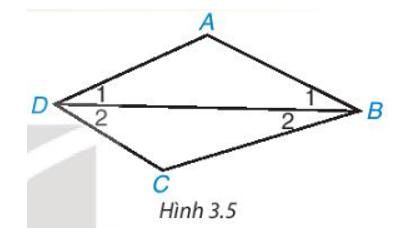
Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng của tứ giác ABCD.
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đoCho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.