Trong một tam giác cân, đường phân giác xuất phát từ đỉnh cũng là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
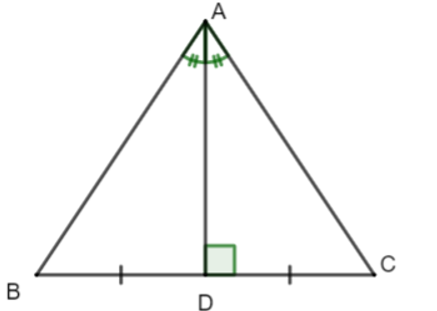
Tam giác ABC cân tại A có đường phân giác AD.
Xét ΔABD và ΔACD có:
AB = AC (ΔABC cân tại A)
= ( AD là đường phân giác )
AD là cạnh chung.
Do đó ΔABD = ΔACD (c.g.c)
Suy ra BD = CD (hai cạnh tướng ứng).
Do đó D là trung điểm của BC (1)
Vậy AD cũng là đường trung tuyến ứng với cạnh BC.
Ta có: = ( ΔABD = ΔACD, hai góc tương ứng).
Mà + = 180°.
Nên 2 = 180° hay = 90°.
Do đó AD vuông góc với BC tại D (2)
Từ (1) và (2) suy ra AD cũng là đường trung trực.
Do vậy cả ba đáp án A, B, C đều đúng.
Cho ∆ABC cân tại A có BD và CE là hai đường phân giác cắt nhau tại F. Tia AF cắt BC tại G. Khi đó điểm G:
Cho ∆ABC có trọng tâm G và I là giao của ba đường phân giác của tam giác ∆ABC. Biết B; G; I thẳng hàng. Khi đó ΔABC là tam giác gì?
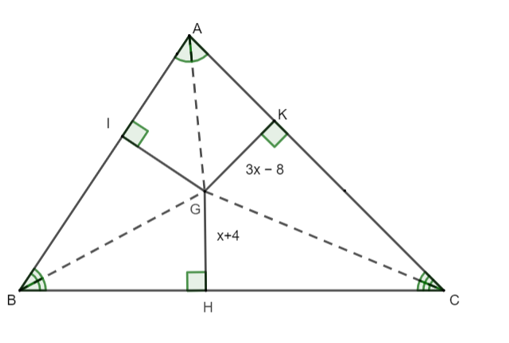
Cho hình vẽ như bên dưới. Biết GI = 8 cm. Độ dài đoạn thẳng GH bằng:
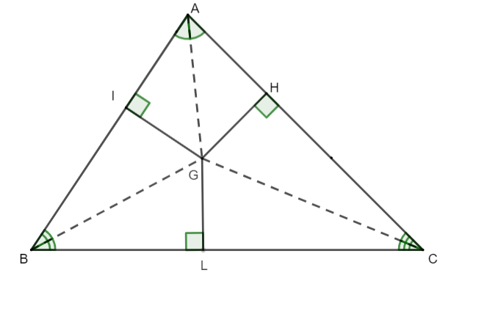
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó:
Điền vào chỗ trống sau: “Ba đường phân giác đi qua một điểm. Điểm này cách đều … của tam giác”.
Cho tam giác ABC có hai đường phân giác AD và BE cắt nhau tại G. Khi đó CG là
Điền vào chỗ trống: “Giao điểm của ba đường phân giác trong một tam giác …”
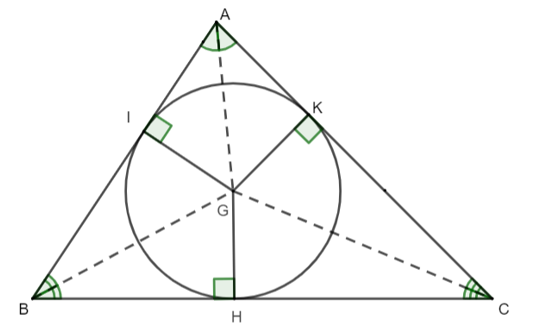
Cho hình vẽ như bên dưới. Biết GK = 3x − 8 và GH = x + 4. Khi đó giá trị của x bằng: