 Giải bởi Vietjack
Giải bởi Vietjack
Hàm số 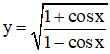
Do đó (1) ⇔ 1 – cos x ≠ 0 ⇔ cos x ≠ 1 ⇔ x ≠ k.2π.
Vậy tập xác định của hàm số là D = R \ {k.2π, k ∈ Z}.
Phương pháp giải
+ Hàm số y = 1/f(x) xác định khi f(x) ≠ 0 .
+ Hàm số y= √(f(x)) xác định khi f(x) ≥ 0.
+ Hàm số y = 1/√(f(x)) xác định khi f(x)> 0
+ Hàm số y= tan [f(x)] xác định khi cos[f(x)] ≠ 0 .
+ Hàm số y = cot [f(x)] xác định khi sin[ f(x)] ≠ 0
+ Hàm số y= tan[ f(x)]+cot[g(x)] xác định khi cos[f(x)] ≠ 0;sin[ g(x)] ≠ 0
* Chú ý:
sinx ≠ 0 ⇔ x ≠ k.π
cosx ≠ 0 ⇔ x ≠ π/2+kπ với k nguyên
sinx ≠ 1 ⇔ x ≠ π/2+k2π và sinx ≠ -1 ⇔ x ≠ -π/2+k2π
cosx ≠ 1 ⇔ x ≠ k2π và cosx ≠ -1 ⇔ x ≠ π+k2π
Tham khảo thêm một số tài liệu liên quan:
Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = |sin x|
Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Dựa vào đồ thị hàm số y = cos x, tìm các giá trị của x để cos x = 1/2
Dựa trên đồ thị hàm số y = sin x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.
Chứng minh rằng sin 2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x
Tìm những số T sao cho f(x + T) với mọi x thuộc tập xác định của hàm số sau:
a) f(x) = sinx;
b) f(x) = tanx.
Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
Sử dụng máy tính bỏ túi, hãy tính sinx, cosx với x là các số sau:
π/6; π/4; 1,5; 2; 3,1; 4,25; 5.