Tìm các giá trị lượng giác của các góc 120o, 150o.

Các giá trị lượng giác của góc 120o là:

sin 120º = sin (180º – 60º) = sin 60º = √3/2.

cos 120º = cos(180º – 60º) = –cos 60º = –1/2

tan 120º = sin 120º / cos 120º = –√3

cot 120º = cos 120º / sin 120º = –1/√3

Các giá trị lượng giác của góc 150º là:

sin 150º = sin ( 180º – 30º ) = sin 30º = 1/2

cos 150º = –cos ( 180º – 30º ) = –cos 30º = (–√3)/2

tan 150º = sin 150º / cos 150º = –1/√3

cot 150º = cos 150º / sin 150º = –√3.

Giá trị lượng giác của một góc

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x₀; y₀) trên nửa đường tròn đơn vị để $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$.

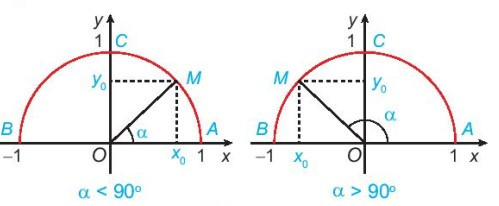
- Định nghĩa tỉ số lượng giác của một góc từ 0^o đến 180^o

Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho  $\widehat{\mathrm{xOM}}=\mathrm{\alpha }$. Khi đó:

+ sin của góc α là tung độ y₀ của điểm M, được kí hiệu là sin α;

+ côsin của góc α là hoành độ x₀ của điểm M, được kí hiệu là cos α;

+ Khi α ≠ 90° (hay x₀ ≠ 0), tang của α là $\frac{{\mathrm{y}}_0}{{\mathrm{x}}_0}$, được kí hiệu là tan α;

+ Khi α ≠ 0° và α ≠ 180° (hay y₀ ≠ 0), côtang của α là $\frac{{\mathrm{x}}_0}{{\mathrm{y}}_0}$, được kí hiệu là cot α.

- Từ định nghĩa trên ta có:

$\mathrm{tan\alpha }=\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}(\mathrm{\alpha }\ne 90°);$$\mathrm{cot\alpha }=\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}(\mathrm{\alpha }\ne 0°\mathrm{và}\mathrm{\alpha }\ne 180°);$$\mathrm{tan\alpha }=\frac{1}{\mathrm{cot\alpha }}\text{ (}\mathrm{\alpha }\notin \text{{}0°;90°;180°\text{}})$

- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:

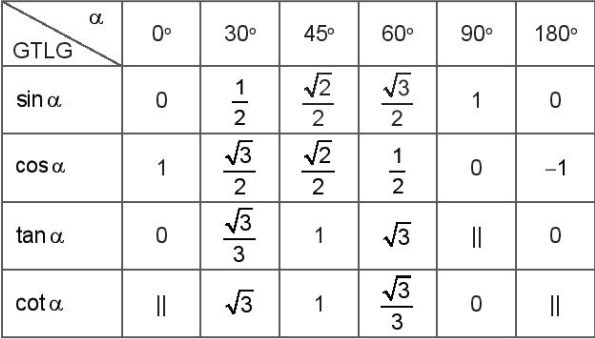
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.

Xem thêm một số kiến thức liên quan:

Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180 (Kết nối tri thức) hay, chi tiết | Toán lớp 10

20 câu Trắc nghiệm Giá trị lượng giác của 1 góc từ 0° đến 180° (Kết nối tri thức) có đáp án – Toán lớp 10