Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
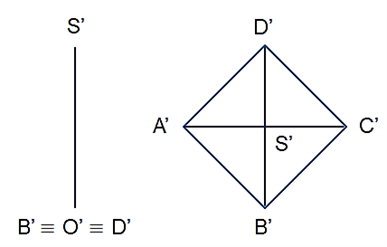
Vì đường thẳng BD vuông góc với mặt phẳng (SAC) nên cũng vuông góc với mặt phẳng hình chiếu đứng (P1). Do đó hình chiếu đứng của ba điểm B, O, D trùng nhau.
Do vậy hình chiếu đứng và hình chiếu bằng của hình chóp S.ABCD trong trường hợp này lần lượt được vẽ như hình dưới đây:
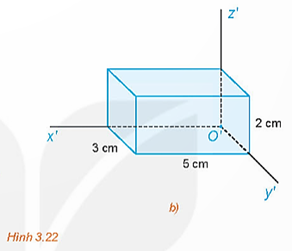
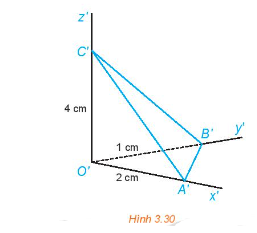
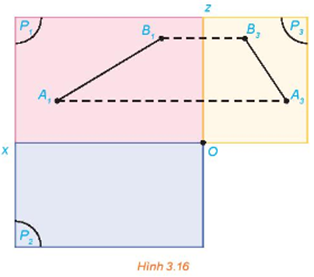
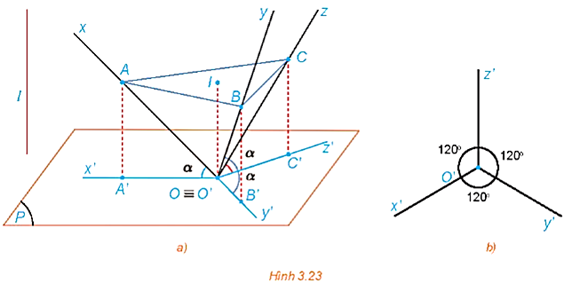
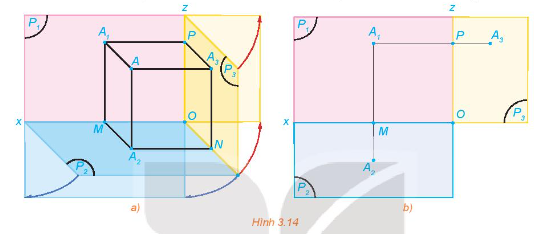
Trong HĐ2, gọi (P3) là mặt phẳng hình chiếu cạnh và A3 là hình chiếu cạnh của A. Gọi Oz là giao tuyến của (P1) và (P3), Oy là giao tuyến của (P2) và (P3). Quay mặt phẳng (P2) quanh Ox sao cho (P2) trùng với (P1) và quay mặt phẳng (P3) quanh Oz sao cho (P3) trùng với (P1), khi đó ba điểm A1, A2, A3 cùng thuộc mặt phẳng (P1) (H.3.14).
a) Đường thẳng A1A3 có vuông góc với đường thẳng Oz hay không? Khoảng cách từ A3 đến Oz có bằng khoảng cách từ A2 đến Ox hay không?
b) Trong mặt phẳng (P1), trình bày cách xác định điểm A3 khi biết hai điểm A1, A2.
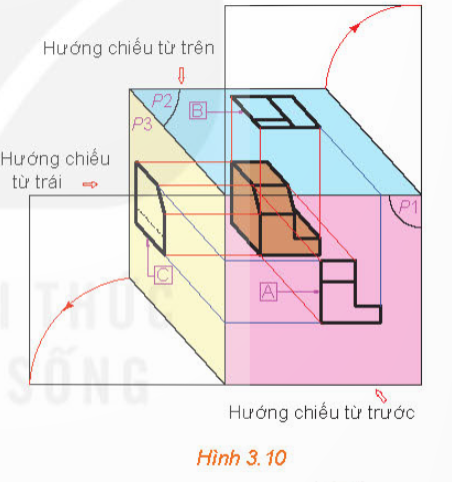
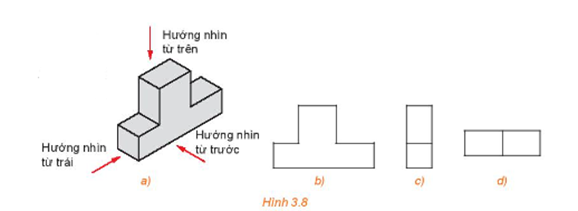
Trong các khẳng định sau, những khẳng định nào là đúng?
a) Hình chiếu đứng của một hình ℋ là hình chiếu song song của hình ℋ lên một mặt phẳng nào đó.
b) Hình chiếu đứng và hình chiếu bằng nằm trong hai mặt phẳng vuông góc với nhau.
c) Hình chiếu cạnh của một đường thẳng luôn là một đường thẳng.
d) Hình chiếu bằng của hai điểm phân biệt luôn là hai điểm phân biệt.