Phương trình có tổng các nghiệm thuộc khoảng bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Ta có
Vì nghiệm của phương trình thuộc nên ta có:
Mà nên ta có k = 0 và k = 1 ứng với các nghiệm: .
Vậy tổng nghiệm của phương trình là
Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện 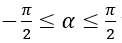
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
Xem thêm một số kiến thức liên quan:
Đề thi tham khảo Toán 2024 có đáp án
Đề thi thử Toán 2024 phát triển từ đề tham khảo
Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h, góc giữa hai mặt phẳng bằng bằng Tính thể tích của khối chóp S.ABCD theo
Cho hình chóp SABC ,gọi M,N lần lượt là trung điểm của SA,SB . Tính tỉ số
Cho đồ thị . Tất cả giá trị của tham số m để cắt trục hoành tại ba điểm phân biệt có hoành độ thỏa
Xác đinh a,b,c để hàm số có đồ thi như hình vẽ bên. Chon đáp án đúng?
Cho hình tứ diện ABCD có M,N lần lượt là trung điểm của AB,BD Các điểm G,H lần lượt trên cạnh AC, CD sao cho NH cắt MG tại I Khẳng định nào sau đây là khẳng định đúng?
Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm O. Chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác xuất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.
Cho tứ diện ABCD có AB,AC,AD, đôi một vuông góc với nhau biết AB=AC=AD=1. Số đo góc giữa hai đường thẳng ABvà CD bằng:
Cho hàm số: có đồ thị (C) Đường thẳng cắt đồ thị (C) tại ba điểm phân biệt Với , giá trị tham số m để tam giác MBC có diện tích bằng là: