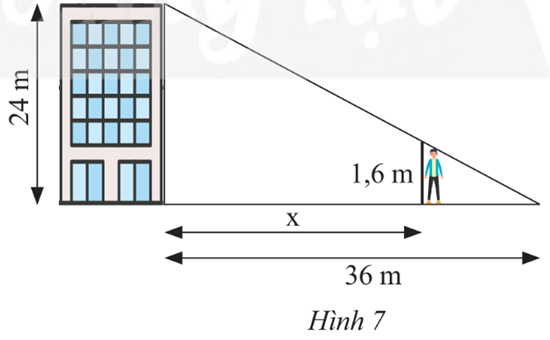
Một tòa nhà cao 24 m, đổ bóng nắng dài 36 m trên đường như Hình 7. Một người cao 1,6 m muốn đứng trong bóng râm của tòa nhà. Hỏi người đó có thể đứng cách tòa nhà xa nhất bao nhiêu mét?
 Giải bởi Vietjack
Giải bởi Vietjack
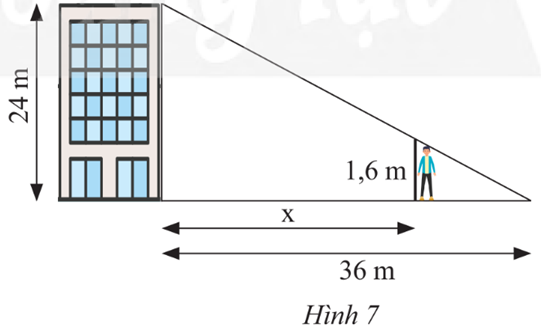
Ta có: , do đó DC = 2,4 (m).
Mà BD + DC = BC suy ra BD = BC – DC hay x = 36 – 2,4 = 33,6 (m).
Vậy người đó có thể đứng cách tòa nhà xa nhất là 33,6 mét.
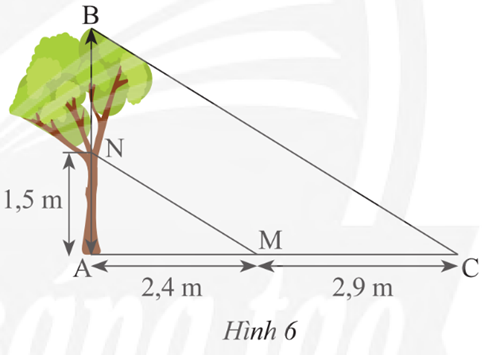
Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong Hình 6. Tìm chiều cao AB của cái cây.
Cho tam giác ABC, biết DE // BC và AE = 6 cm, EC = 3 cm, DB = 2 cm (Hình 1). Độ dài đoạn thẳng AD là
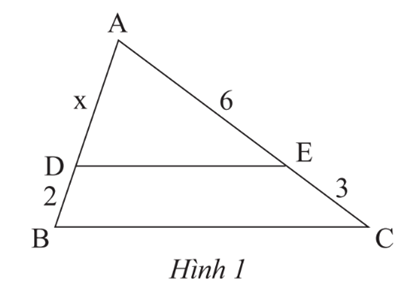
A. 4 cm
B. 3 cm
C. 5 cm
D. 3.5 cm
Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC).
a) Tính độ dài các đoạn thẳng MN và EF.
Cho tam giác MNP có MD là tia phân giác của góc M (D ∈ NP). Trong các khẳng định sau, khẳng định nào đúng?
A.
B.
C.
D.
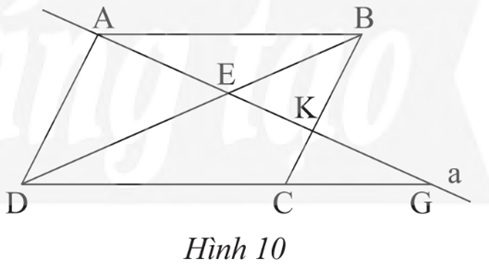
Cho hình bình hành ABCD. Đường thẳng a đi qua A cắt BD, BC, DC lần ượt tại E, K, G (Hình 10). Chứng minh rằng:
a) AE2 = EK.EG.
Cho Hình 4, biết MN // BC, AN = 4 cm. NC = 8 cm, MN = 5 cm. Độ dài cạnh BC là
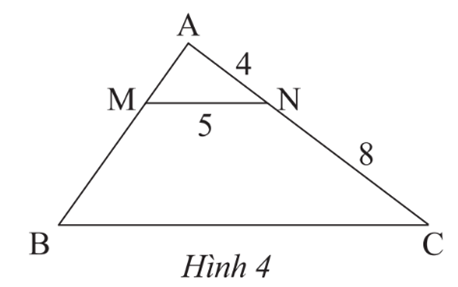
A. 10 cm.
B. 20 cm.
C. 15 cm.
D. 16 cm.
Cho tam giác ABC, một đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. Qua E kẻ đường thẳng song song với CD cắt AB tại F. Biết AB = 25 cm, AF = 9 cm, EF = 12 cm, độ dài đoạn DC là
A. 25 cm
B. 20 cm
C. 15 cm
D. 12 cm
Cho Hình 3, biết AM = 3 cm, MN = 4 cm, AC = 9 cm. Giá trị của biểu thức x – y là:
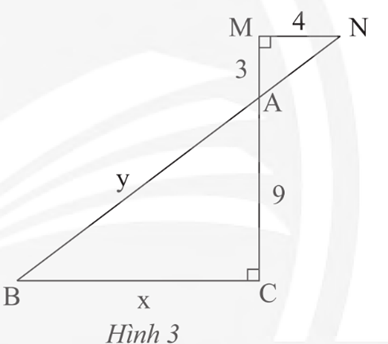
A. 4.
B. – 3.
C. 3.
D. – 4.
Cho tứ giác ABCD có AC và BD cắt nhau tại O. Qua O, kẻ đường thẳng song song với BC cắt AB tại E, kẻ đường thẳng song song với CD cắt AD tại F.
a) Chứng minh FE // BD;
b) Từ O kẻ đường thẳng song song với AB cắt BC tại G và đường thẳng song song với AD cắt CD tại H. Chứng minh rằng CG.DH = BG.CH.
b) Dựa vào kết quả của câu a, hãy nêu cách vẽ đường phân giác của một góc trong tam giác bằng đường kẻ và êke.