Lớp 10A của trường có 20 học sinh thích môn Toán, 18 học sinh thích môn Ngữ văn và 10 học sinh thích cả môn Toán và Ngữ văn. Hỏi lớp 10A có bao nhiêu học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ văn?

Cho A = (2; +∞) và B = (m; +∞). Điều kiện cần và đủ của m để B là tập con của A là:

Cho hai tập hợp A = {x ∈ ℝ| (2x – x²)(2x² – 3x – 2) = 0} và B = {n ∈ ℕ| 3 < n² < 30}, chọn mệnh đề đúng:

“Nếu a và b là hai số hữu tỉ thì tổng a + b cũng là số hữu tỉ”. Cách phát biểu nào sau đây diễn đạt mệnh đề trên?

Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

Trong các tập hợp sau đây, tập hợp nào có đúng hai tập con:

Mệnh đề chứa biến: “x³ – 3x² + 2x = 0” đúng với giá trị nào của x?

Cho A là tập hợp các tứ giác lồi, B là tập hợp các hình thang, C là tập hợp các hình bình hành, D là tập hợp các hình chữ nhật, E là tập hợp các hình thoi và F là tập hợp các hình vuông

Xét các câu sau:

(I). E ⊂ F ⊂ D ⊂ B ⊂ A.

(II). F ⊂ E ⊂ C ⊂ B ⊂ A.

(III). F ⊂ D ⊂ E ⊂ B ⊂ A.

Câu nào đúng?

Cho hai tập hợp A = {1; 2; a; b} và B = {1; x; y} với x, y khác a, b, 1, 2. Kết luận nào sau đây là đúng?

Trong các mệnh đề sau, mệnh đề nào đúng?

Nếu A và B là tập hợp hữu hạn thì công thức nào sau đây đúng?

Trong các câu sau, câu nào sai?

Cho các tập hợp A, B, C được minh hoạ bằng biểu đồ Ven như hình vẽ dưới đây:

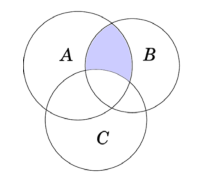
Phần tô màu xám trong hình vẽ biểu diễn của tập hợp nào sau đây?

Cho 3 tập hợp E, F, G sao cho E ⊂ F, F ⊂ G và G ⊂ E. Câu nào sau đây đúng?