Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau:
v(t) = 0,001302t3 – 0,09029t2 + 23,
(v được tính bằng ft/s, 1 feet = 0,3048 m)
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Giải bởi Vietjack
Xét hàm số vận tốc của tàu con thoi v(t) = 0,001302t3 – 0,09029t2 + 23 với t ∈ [0; 126].
Gia tốc của tàu con thoi là a(t) = v'(t) = 0,003906t2 – 0,18058t.
Ta có a'(t) = 0,007812t – 0,18058
a'(t) = 0 ⇔ t ≈ 23.
Bảng biến thiên của hàm số a(t) như sau:
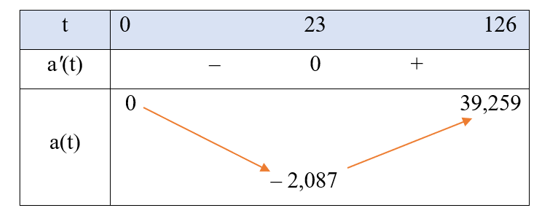
Vậy gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian (23 s; 126 s) tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi.
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (0 ≤ x ≤ 300) được cho bởi hàm số y = – x3 + 300x2 (đơn vị: nghìn đồng) và được minh họa bằng đồ thị ở Hình 1.
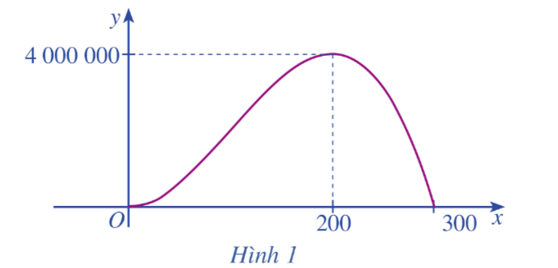
Sự thay đổi lợi nhuận theo số sản phẩm sản xuất ra và dấu của đạo hàm y' có mối liên hệ với nhau như thế nào?
Thể tích V (đơn vị: centimét khối) của 1 kg nước tại nhiệt độ T (0 °C ≤ T ≤ 30 °C) được tính bởi công thức sau:
V(T) = 999,87 – 0,06426T + 0,0085043T2 – 0,0000679T3.
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)
Hỏi thể tích V(T), 0 °C ≤ T ≤ 30 °C, giảm trong khoảng nhiệt độ nào?
Cho hai hàm số y = f(x), y = g(x) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
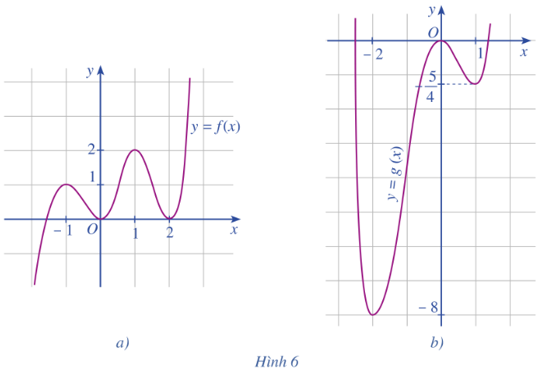
Tìm điểm cực trị (nếu có) của mỗi hàm số sau:
a) y = x4 – 32x + 1;
b) .
Chứng minh rằng hàm số nghịch biến trên nửa khoảng (– ∞; 0] và đồng biến trên nửa khoảng [0; + ∞).
Tìm các khoảng đơn điệu của mỗi hàm số sau:
a) y = – x3 + 2x2 – 3;
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập K ⊂ ℝ, trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số y = f(x) = x2 có đồ thị như Hình 2.
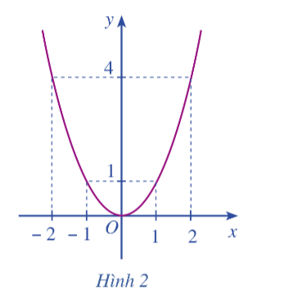
Xác định khoảng đồng biến, nghịch biến của hàm số đó.
Xét dấu của đạo hàm f'(x) = 2x.
Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số f(x) = x2 và dấu của đạo hàm f'(x) = 2x trên mỗi khoảng (– ∞; 0), (0; + ∞).
Hoàn thành bảng biến thiên sau
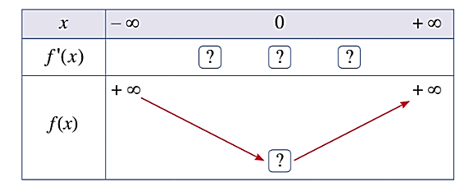
Cho hàm số y = f(x) có bảng biến thiên như sau:
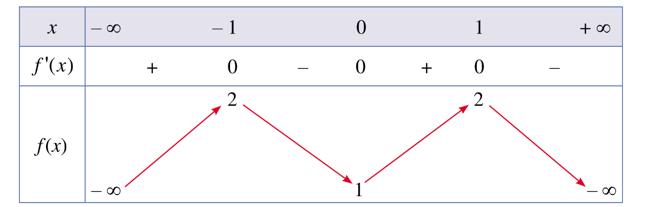
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (1; + ∞).
B. (– 1; 0).
C. (– 1; 1).
D. (0; 1).
Tìm các khoảng đơn điệu của mỗi hàm số sau:
b) y = x4 + 2x2 + 5;
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
