Hỏi hàm số y = f (x) đồng biến trên khoảng nào dưới đây...

Question

Hình dưới là đồ thị hàm số y = f'(x). Hỏi hàm số y = f (x) đồng biến trên khoảng nào dưới đây?

VietJack · Accepted Answer

Đáp án cần chọn là: C Hàm số y = f'(x) dương trong khoảng 2;+∞ => hàm số y=fx đồng biến trên 2;+∞ Các bước xét tính đơn điệu của hàm số y = f(x) Bước 1. Tìm tập xác định của hàm số y = f(x). Bước 2. Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, …, n) mà tại đó đạo hàm bằng 0 hoặc không tồn tại. Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên của hàm số. Bước 4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số. Bài tập liên quan: Cho hàm số y=f(x)y=fx có đồ thị như hình vẽ. 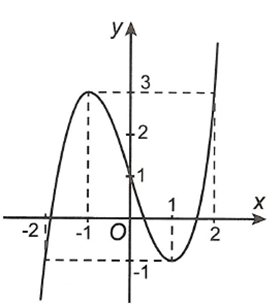Hàm số đã cho đồng biến trên khoảng dưới đây nào A. (-2;2) B. (0;2) C. (-1;1) D. (1;2) Hướng dẫn giải: - Xét đáp án A, trên khoảng (−1;1)⊂(−2;2)−1;1⊂−2;2 đồ thị hướng đi xuống hay hàm nghịch biến trên khoảng đó. - Xét đáp án B, trên khoảng (0;1)⊂(0;2)0;1⊂0;2 đồ thị có đoạn hướng đi xuống hay hàm số nghịch biến trên đó. - Xét đáp án C, trên khoảng (−1;1)−1;1 đồ thị có hướng đi xuống hay hàm số nghịch biến trên khoảng đó. - Xét đáp án D, trên khoảng (1;2)1;2 đồ thị có hướng đi lên hay hàm số đồng biến trên khoảng đó nên chọn. Chọn D. Tham khảo thêm một số tài liệu liên quan: Trắc nghiệm Sự đồng biến, nghịch biến của hàm số Bài tập trắc nghiệm về tính đơn điệu của hàm số chứa tham số m

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Hình dưới là đồ thị hàm số $y = f' (x)$ . Hỏi hàm số y = f (x) đồng biến trên khoảng nào dưới đây?

A. $(0; 1); (2; + \infty)$

B. $(1; 2)$

C. $(2; + \infty)$

D. $(0; 1)$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Hàm số $y = \frac{x^{4}}{4} - 2 x^{2} + 3$ nghịch biến trên khoảng nào?

Câu 2:

Hàm số $y = - x^{4} - 2 x^{2} + 3$ nghịch biến trên:

Câu 3:

Hàm số $y = 2 x^{3} - 9 x^{2} + 12 x + 3$ nghịch biến trên những khoảng nào?

Câu 4:

Cho hàm số $y = x^{4} - 2 x^{2} + 15$ . Hàm số đồng biến trên khoảng nào dưới đây?

Câu 5:

Hàm số $y = - x^{3} + 3 x^{2} - 1$ đồng biến trên khoảng

Câu 6:

Trong các hàm số dưới đây, hàm số nào không đồng biến trên R?

Câu 7:

Cho hàm số $y = f (x)$ xác định và liên tục trên R và có đạo hàm $f' (x) = x^{2} - 4$ . Chọn khẳng định đúng:

Câu 8:

Cho hàm số $y = - x^{4} + 2 x^{3} - 2 x - 1$ nghịch biến trên khoảng nào sau đây?

Câu 9:

Hàm số $y = 2 x^{4} + 1$ đồng biến trên khoảng nào?

Câu 10:

Cho hàm số $y = f (x)$ xác định và liên tục trên R và có đạo hàm $f' (x) = - x^{2} + 4$ . Chọn khẳng định đúng:

Câu 11:

Cho hàm số $y = x^{3} - 3 x^{2} + 5$ . Mệnh đề nào dưới đây đúng?

Câu 12:

Hàm số $y = x^{3} - 3 x^{2} + 4$ đồng biến trên:

Câu 13:

Cho hàm số $f (x) = - 2 x^{3} + 3 x^{2} + 12 x - 5$ . Trong các mệnh đề sau, tìm mệnh đề sai?

Câu 14:

Tìm tất cả các khoảng đồng biến của hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 3 x - 1$ ?

Đề thi liên quan

Câu hỏi mới nhất

Câu hỏi:

Hình dưới là đồ thị hàm số y = f'(x). Hỏi hàm số y = f (x) đồng biến trên khoảng nào dưới đây?

A. 0;1;2;+∞

B. 1;2

C. 2;+∞

D. 0;1