Hàm số (m là tham số thực) đạt giá trị lớn nhất trên [0;1] là 1 khi
A. m = 1
B. m = 0
C. m = -1
D. m = 2
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Tìm GTLN, GTNN của hàm số trên 1 đoạn.
Phương pháp giải.
Phương pháp: Cho hàm số y = f(x) xác định và liên tục trên [a,b] .
Bước 1. Tính đạo hàm f'(x) .
Bước 2. Tìm tất cả các nghiệm xi ∈ [a,b] của phương trình f'(x) = 0 và tất cả các điểm αi ∈ [a,b] làm cho f'(x) không xác định.
Bước 3. Tính f(a), f(b), f(xi), f(αi).
Bước 4. So sánh các giá trị tính được và kết luận 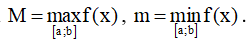
Lưu ý:
- Đối với bài toán tìm GTLN, GTNN trên khoảng, nửa đoạn làm tương tự.
- Trong trường hợp trên khoảng đó không tồn tại giá trị f’(x) = 0 hoặc không xác định thì kết luận không tìm được GTLN, GTNN trên khoảng đó.
Bài tập liên quan:
Gọi m là số thực để hàm số y= (x+ m)3 đạt giá trị lớn nhất bằng 8 trên đoạn [1; 2]. Khẳng định nào dưới đây đúng?
A. -2< m< 0
B. 2< m< 4
C. -1< m< 2
D. 0 <m< 3
Lời giải chi tiết:
Ta có đạo hàm y’ = 3( x+ m)2≥0 với mọi x.
=> Hàm số đồng biến trên đoạn [1; 2] nên hàm số đạt GTLN tại x = 2.
Khi đó; y(2) = 8 khi và chỉ khi : (2+m)3 = 8 hay m= 0
Chọn C.
Tham khảo thêm một số tài liệu liên quan:
Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho Góc giữa đường thẳng SB và (ABC) là
Cho hình chóp S.ABC có và đáy là tam giác ABC cân tại A. Biết và BC = 2a. Thể tích khối chóp S.ABC là
Người ta định xây dựng một trạm biến áp 110Kv tại ô đất C đường quốc lộ MN để cấp điện cho hai khu công nghiệp A và B như hình vẽ. Hai khu công nghiệp A và B cách quốc lộ lần lượt là AM = 3km, BN = 6km. Biết rằng quốc lộ MN dài 12km. Hỏi phải đặt trạm biến áp cách khu công nghiệp A bao nhiêu km để tổng chiều dài đường dây cấp điện cho hai khu công nghiệp A và B là ngắn nhất
Cho hàm số có đồ thị (C), đồ thị y = f '(x) như hình vẽ bên. Biết đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng . Tính bằng?
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SC tạo với mặt phẳng đáy (ABCD) một góc Thể tích khối chóp S.ABCD theo a là
Trong không gian cho tam giác ABC vuông tại A, AB=2a và ACB = . Thể tích V của khối nón nhận được khi quay tam giác ABC quanh cạnh AC là
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB, E là trung điểm của CB, I là giao điểm của AE và BD. Khi đó IG sẽ không song song với mặt phẳng nào dưới đây?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông góc với đáy và SA = 2a. Khoảng cách giữa hai đường thẳng AB và SC là
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, các cạnh bên bằng 2a. Gọi M là trung điểm SB, N là điểm trên cạnh SC sao cho SN=3NC. Thể tích khối chóp A.BCNM có giá trị nào sau đây?
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và đường thẳng y = 2x là