Viết phương trình mặt phẳng: Đi qua A(0; -1; 2) và song song với giá của mỗi vec tơ = (3; 2; 1) và = (-3; 0; 1).
 Giải bởi Vietjack
Giải bởi Vietjack
Mặt phẳng nhận và là vec tơ chỉ phương
⇒ nhận 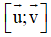
Mặt phẳng đi qua A(0 ; -1 ; 2) nên có phương trình :
2(x – 0) – 6(y + 1) + 6(z – 2) = 0
⇔ 2x – 6y + 6z – 18 = 0
⇔ x – 3y + 3z – 9 = 0.
Trong không gian Oxyz cho ba điểm A(2; -1; 3), B(4; 0; 1), C(-10; 5; 3). Hãy tìm tọa độ một vecto pháp tuyến của mặt phẳng (ABC).
Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 3; 7), B(4; 1; 3)
Lập phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
Viết phương trình mặt phẳng: Đi qua ba điểm A(-3; 0; 0); B(0; -2; 0) và C(0; 0; -1).
Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau: 2x – y + 2z – 9 = 0 (α)
Lập phương trình mặt phẳng (α) qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng ( β) : 2x – y + z – 7 = 0
Viết phương trình mặt phẳng:
Đi qua điểm M(1; -2; 4) và nhận = (2 ; 3 ; 5) làm vec tơ pháp tuyến
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
Hãy tìm một vecto pháp tuyến của mặt phẳng (α): 4x – 2y - 6z +7 = 0.
Cho hai mặt phẳng (α) và (β) có phương trình
(α): x - 2y + 3z + 1 = 0
(β): 2x – 4y + 6z + 1 = 0.
Có nhận xét gì về vecto pháp tuyến của chúng ?
Lập phương trình của các mặt phẳng đi qua điểm M(2; 6; -3) và lần lượt song song với các mặt phẳng tọa độ.